 Low |
 Medium |
 Tall |
 Sparse |
 Dense |
 Very Dense |
 Regular |
 Irregular |
 Random |
(b)
Note: Work described within is a summary of a paper that was published in Proceedings IEEE Visualization '98; a PDF version of the paper is available for downloading.
CR Categories: H.5.2 [Information Interfaces and Presentation]: User Interfaces - ergonomics, screen design, theory and methods; I.3.6 [Computer Graphics]: Methodology and Techniques - ergonomics, interaction techniques; J.2 [Physical Sciences and Engineering]: Earth and Atmospheric Sciences
Keywords: computer graphics, experimental design, human vision, multidimensional dataset, perception, preattentive processing, scientific visualization, texture, typhoon
We use perceptual texture elements (or pexels) to represent values in our dataset. Our texture elements are built by varying three separate texture dimensions: height, density, and regularity. Density and regularity have been identified in the computer vision literature as being important for performing texture segmentation and classification [Rao93b, Rao93a, Tam78]. Moreover, results from cognitive psychology have shown that all three dimensions are detected by the low-level human visual system [Aks96, Jul81b, Tri85, Wol94]. We conducted a set of controlled experiments to measure user performance, and to identify visual interference that may occur between the three texture dimensions during visualization. The result is a collection of pexels that allow a user to visually explore a multidimensional dataset in a rapid, accurate, and relatively effortless fashion.
Section 2 describes research in computer vision, cognitive psychology, and computer graphics that has studied methods for identifying and controlling the properties of a texture pattern. Section 3 explains how we built our perceptual texture elements. Section 4 discusses the experiments we used to test our pexels, and the results we obtained. Finally, in Section 5 we show how our work was used to visualize typhoon conditions in eastern Asia during the summer and fall of 1997.
Researchers have used different methods to study the perceptual features inherent in a texture pattern. Bela Julész [Jul81b] conducted numerous experiments that investigated how a texture's first, second, and third-order statistics affect discrimination in the low-level human visual system. This led to the texton theory [Jul84], which suggests that early vision detects three types of features (or textons, as Julész called them): elongated blobs with specific visual properties (e.g., hue, orientation, and width), ends of line segments, and crossings of line segments. Tamura et al. [Tam78] and Rao and Lohse [Rao93b, Rao93a] identified texture dimensions by conducting experiments that asked subjects to divide pictures depicting different types of textures (Brodatz images) into groups. Tamura et al. used their results to propose methods for measuring coarseness, contrast, directionality, line-likeness, regularity, and roughness. Rao and Lohse used multidimensional scaling to identify the primary texture dimensions used by their subjects to group images: regularity, directionality, and complexity. Haralick et al. [Har73] built greyscale spatial dependency matrices to identify features like homogeneity, contrast, and linear dependency. These features were used to classify satellite images into categories like forest, woodlands, grasslands, and water. Liu and Picard [Liu94] used Wold features to synthesize texture patterns. A Wold decomposition divides a 2D homogeneous pattern ( e.g., a texture pattern) into three mutually orthogonal components with perceptual properties that roughly correspond to periodicity, directionality, and randomness. Malik and Perona [Mal90] designed computer algorithms that use orientation filtering, nonlinear inhibition, and computation of the resulting texture gradient to mimic the discrimination ability of the low-level human visual system. We used these results to choose the perceptual texture dimensions we wanted to investigate during our experiments.
Work in computer graphics has studied methods for using texture patterns to display information during visualization. Schweitzer [Sch83] used rotated discs to highlight the orientation of a three-dimensional surface. Pickett and Grinstein [Gri89] built "stick-men" icons to produce texture patterns that show spatial coherence in a multidimensional dataset. Ware and Knight [War92, War95] used Gabor filters to construct texture patterns; attributes in an underlying dataset are used to modify the orientation, size, and contrast of the Gabor elements during visualization. Turk and Banks [Tur96] described an iterated method for placing streamlines to visualize two-dimensional vector fields. Interrante [Int97] displayed texture strokes to help show three-dimensional shape and depth on layered transparent surfaces; principal directions and curvatures are used to orient and advect the strokes across the surface. Finally, Salisbury et al. [Sal97] and Wikenbach and Salesin [Win96] used texturing techniques to build computer-generated pen-and-ink drawings that convey a realistic sense of shape, depth, and orientation. We built upon these results to try to develop an effective method for displaying multidimensional data through the use of texture.
Our visualization technique should allow rapid, accurate, and relatively effortless visual analysis on the resulting images. This can be accomplished by exploiting the human visual system. The low-level visual system can perform certain exploratory analysis tasks (e.g., target identification, boundary detection, region tracking, and estimation) very rapidly and accurately, without the need for focused attention [Hea96c, Hea96a]. These tasks are often called "preattentive", because their completion precedes attention in the visual system [Tri85, Wol94]. More importantly, preattentive tasks are independent of display size; an increase in the number of elements in the display causes little or no increase in the amount of time required to complete the analysis task. Unfortunately, preattentive visualization tools cannot be built by mapping data attributes to visual features in an ad-hoc fashion. Certain combinations of visual features will actively interfere with the low-level visual system, making it much more difficult to complete the corresponding visualization task. Any technique that depends on the low-level visual system must be designed to avoid this kind of interference.
Within this framework, we decided to focus on the following three questions during our study:
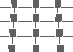
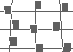
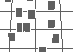
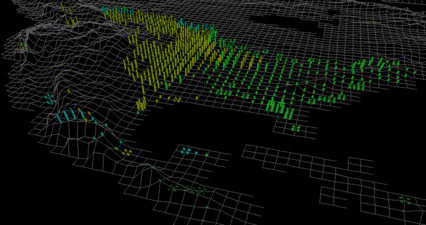
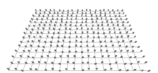
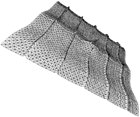
In order to support variation of height, density, and regularity, we built pexels that look like a collection of paper strips. The user maps attributes in the dataset to the density (which controls the number of strips in a pexel), height, and regularity of each pexel. Unlike Gabor filters or Wold features, which require some expertise to manipulate, our elements allow a user to understand clearly how changing a particular texture dimension affects the appearance of a pexel. Examples of each of these perceptual dimensions are shown in Figure 1a. Figure 1b shows an environmental dataset being visualized with texture and color. Locations on the map that contain pexels represent areas in North and Central America with high levels of cultivation. Three discrete heights show the level of cultivation (short for 50-74% cultivated, medium for 75-99%, and tall for 100%), density shows the ground type (sparse for alluvial, dense for wetlands), and color shows the vegetation type (yellow for plains, green for forest, cyan for woods, and purple for shrubland). A method described by Healey [Hea96c] was used to ensure all colors are equally distinguishable from one another (note that printed colors do not match exactly the on-screen colors used to display the map). Users can easily identify medium height pexels that correspond to lower levels of cultivation in the central and eastern plains; short pexels can be seen along the spine of Central America. Areas containing wetlands can be seen as dense pexels in Florida, along the eastern coast, and in the southern parts of the Canadian prairies.
 Low |
 Medium |
 Tall |
 Sparse |
 Dense |
 Very Dense |
 Regular |
 Irregular |
 Random |

(b)
Figure 1: Groups of paper strips are used to form a pexel that supports variation of the three perceptual texture dimensions height, density and randomness: (a) each pexel has one of its dimensions varied across three discrete values; (b) a map of North America, pexels represent areas of high cultivation, height mapped to level of cultivation, density mapped to ground type, color mapped to vegetation type
Height and density both have a natural ordering that can be used for our purposes. Specifically, pexels with shorter strips come before pexels with taller ones, and pexels that are sparse (i.e., pexels that contain fewer paper strips) come before pexels that are dense.
Ordering regularity requires a more complete explanation. Although regularity is an intuitive concept, specifying it mathematically is not as straightforward. Researchers who used regularity as one of their primary texture dimensions have shown that differences in regularity cause a difference in second-order statistics that is detected by the visual system. Image correlation is one method of measuring second-order statistics. Two images can be completely correlated if there exists a translation that shifts one image into a position where its pixels exactly match the pixels in a second image. The amount of correlation between two images at a given offset can also be measured. Suppose an image A, with a width of N and a height of M pixels, is offset into a second image B, with the upper left corner of A at position (t,u) in B. The correlation of A into B at position (t,u) is then
C(t,u) = 1 / K [ sum(x=1,N) sum(y=1,M) ( A(x,y) - A_Avg ) * ( B(x+t,y+u) - B_Avg ) ]
where
K = N * M * sqrt( A_Var ) * sqrt( B_Var )
and
A_Avg = 1 / (N * M) [ sum(x=1,N) sum(y=1,M) A(x,y) ]
A_Var = 1 / (N * M) [ sum(x=1,N) sum(y=1,M) ( A(x,y) - A_Avg )^2 ]
and similarly to compute B_Avg and B_Var. The same technique can be used to measure regularity in a single image, by correlating the image with itself (also known as autocorrelation). Intuitively, if an image can be shifted in various ways so it exactly matches with itself, then the image is made up of a regularly repeating pattern. If this cannot be done, then the image is irregular. Images that are more irregular will always be farther from an exact match, regardless of the offset chosen. We define regularity to be the highest correlation peak in an autocorrelated graph (not including shift position (0,0) since C(0,0)=1.0 for every autocorrelated image).
As a practical example, consider Figure 2a (pexels on a regular underlying grid), Figure 2b (pexels on an irregular grid), and Figure 2c (pexels on a random grid). Autocorrelation was computed on the orthogonal projection of each image. A 5 x 3 patch from the center of the corresponding autocorrelation graph is shown beneath each of the three grids. Results in the graphs mirror what we see in each display, that is, as randomness increases, peaks in the autocorrelation graph decrease in height. In Figure 2a peaks of height 1.0 appear at regular intervals in the graph. Each peak represents a shift that places pexels so they exactly overlap with one another. The rate of increase towards each peak differs in the vertical and horizontal directions because the elements in the graph are rectangles (i.e., taller than they are wide), rather than squares. In Figure 2b the graph has the expected sharp peak at (0,0). It also has gentle peaks at shift positions that realign the grid with itself. The peaks are not as high as for the regular grid, because the pexels no longer align perfectly with one another. The sharp vertical and horizontal ridges in the graph represent positions where the underlying grid lines exactly overlap with one another (the grid lines showing the original position of each pexel are still regular in this image). The height of each gentle peak ranges between 0.3 and 0.4. Increasing randomness reduces again the height of the peaks in the correlation graph. In Figure 2c no peaks are present, apart from (0,0) and the sharp ridges that occur when the underlying grid lines overlap with one another. The resulting correlation values suggests that this image is "more random" than either of its predecessors.

|
|

|
 (a) |
 (b) |
 (c) |
Figure 2: Three displays of pexels with different regularity and a 5 x 3 patch from the corresponding autocorrelation graphs: (a) a completely regular display, resulting in sharp peaks of height 1.0 at regular intervals in the autocorrelation graph; (b) a display with irregularly-spaced pexels, peaks in the graph are reduced to a maximum height between 0.3 and 0.4; (c) a display with randomly-spaced pexels, resulting in a completely flat graph except at (0,0) and where underlying grid lines overlap
Examples of two display types are shown in Figure 3. Both displays include target pexels. Figure 3a contains a 2 x 2 target group of medium pexels in a sea of short pexels. The density of each pexel varies across the array, producing an underlying density pattern that is clearly visible. This display type simulates two dimensional data elements being visualized with height as the primary texture dimension and density as the secondary texture dimension. Figure 3b contains a 2 x 2 target group of regular pexels in a sea of random pexels, with a no background texture pattern. The taller target in Figure 3a is very easy to find, while the regular target in Figure 3b is almost invisible.
 (a) |
 (b) |
Figure 3: Two display types from the taller and regular pexel experiments: (a) a target of medium pexels in a sea of short pexels with a background density pattern (2 x 2 target group located left of center); (b) a target of regular pexels in a sea of irregular pexels with no background texture pattern (2 x 2 target group located 8 grids step right and 2 grid steps up from the lower-left corner of the array)
The heights, densities, and regularities we used were chosen through a set of pilot studies. Two patches were placed side-by-side, each displaying a pair of heights, densities, or regularities. Viewers were asked whether the patches were easily discriminable from one another. We tested a range of values for each dimension, although the spatial area available for an individual pexel during our experiments limited the maximum amount of density and irregularity we were able to display. The final values we chose could be rapidly and accurately identified in this limited setting.
The experiments used to test the other five target types (shorter, sparser, denser, more regular, and more irregular) were designed in a similar fashion, with one exception. Experiments that tested regularity had only one target-background pairing: a target of regular pexels in a sea of random pexels (for regular targets), or random pexels in a sea of regular pexels (for irregular targets). Our pilot studies showed that users had significant difficulty discriminating an irregular patch from a random patch. As mentioned above, this was due in part to the small spatial area available to each pexel. Although restricting our regularity conditions to a single target-background pairing meant there were only 18 different display types, users were still asked to complete 576 trials. Thirty-two variations of each display type were shown, 16 of which contained the target pexels, 16 of which did not.
Thirty-eight users (10 males and 28 females) ranging in age from 18 to 26 with normal or corrected acuity participated as observers during our studies. Twenty-four subjects (six per condition) completed the taller, shorter, denser, and regular conditions. Fourteen subjects (seven per condition) completed the sparser and irregular conditions. Subjects were told before the experiment that half the trials would contain a target, and half would not. We used a Macintosh computer with an 8-bit color display to run our studies. Responses (either "target present" or "target absent") for each trial an observer completed were recorded for later analysis.
 (a) |
(b) |
 (c) |
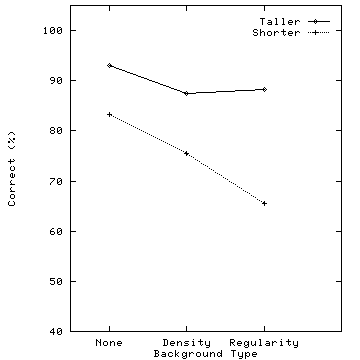
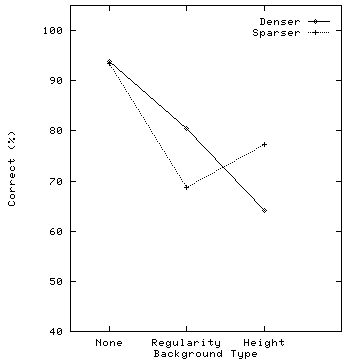
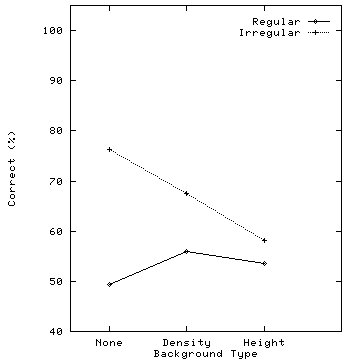
Figure 4: Graphs showing the percentage of correct target detection responses for the six target types, horizontal axis represents background texture pattern, vertical axis represent percentage of correct responses: (a) results for taller and shorter targets; (b) results for denser and sparser targets; (c) results for regular and irregular targets
Taller targets were identified preattentively with very high accuracy (Figure 4a). Background density and regularity patterns caused no significant interference (F(2,10)=4.165, p=0.292). Although accuracy for shorter targets was somewhat lower, it was still acceptable when there was either no background texture pattern or a density texture pattern (83% and 75%, respectively). Both background regularity and density caused a statistically significant reduction in performance (F(2,10)=25.965, p=0.0001). Results showing taller targets were "more salient" than shorter targets was not unexpected; similar asymmetries have been documented by both Triesman [Tri85] and Aks and Enns [Aks96].
As with height, dense in sparse targets were easier to identify than sparse in dense, particularly with a background regularity pattern. Accuracy with no background texture pattern was as high as for taller targets (Figure 4b). In both cases, a significant interference effect occurred when a background texture was present (F(2,10)=77.007, p=0.0001 and F(2,10)=43.343, p=0.0001 for denser and sparser targets, respectively). Height reduced accuracy dramatically for denser targets, while both height and regularity interfered with the identification of sparser targets.
Performance was poorest for regular and irregular targets. Accuracy for irregular targets was reasonable (approximately 76%) when there was no background texture pattern. Results were significantly lower for displays which contained a variation in either density or height (F(2,12)=7.147, p=0.0118, with correct responses of 68% and 58%, respectively). Observers were completely unable to detect regular targets in a sea of irregular pexels (see also Figure 3b). Even with no background texture pattern, correct responses were only 49%. Similar near-chance results (i.e., correct responses of 50%) occurred when height and regularity texture patterns were displayed. We concluded that subjects resorted to guessing whether the target was present or absent.
For target group sizes, results showed that 4 x 4 targets are significantly easier to find than 2 x 2 targets for four target types: taller, shorter, denser and sparser (F(1,4)=20.067, p=0.0009, F(1,4)=93.607, p=0.0001, F(1,4)=26.506, p=0.0003, and F(1,4)=8.041, p=0.014, respectively). There were no significant within-condition F-values, suggesting the effect of target group size (larger easier than smaller) was consistent for each display type. Finally, only shorter and sparser targets showed any significant effect of display duration (F(2,10)=25.965, p=0.0001 and F(2,10)=43.343, p=0.0001, respectively). Again, there were no within-condition F-values; increasing the display duration for shorter or sparser targets resulted in a consistent increase in performance, regardless of the display type being shown.
 (a) |
 (b) |
Figure 5: Two displays with a regular target, both displays should be compared with the target shown in Figure 3b: (a) larger target, an 8 x 8 target in a sea of sparse pexels (target group located above and left of center); (b) denser background, a 2 x 2 target in a sea of dense pexels (target group located below and left of center)
One way to make regularity targets easier to identify is by increasing the size of the target patch. For example, Figure 5a shows an 8 x 8 regular target in a sea of random pexels. This target is much easier to find, compared to the 2 x 2 patch shown in Figure 3b. Unfortunately, we cannot guarantee that the values in a dataset will form large, spatially coherent patches during visualization, although there may be cases where this restriction is acceptable. For example, a secondary attribute displayed with regularity would allow a user to search for large areas of coherence in that attribute's value. This search would normally occur only when the values of a primary attribute (encoded with a preattentively salient feature like height, density, or color) cause the user to stop and perform more in-depth analysis at a particular location in the dataset.
The salience of a regular (or irregular) group of pexels can also be improved by increasing every pexel's density. Figure 5b shows a 2 x 2 regular target in a sea of random pexels, where each pexel is very dense. Again, this target is easier to find than the target in Figure 3b. Unfortunately, this also restricts our visualization system, since density must be constrained to be very dense across the array. In essence, we have lost the ability to vary density over any easily identifiable range. This reduces the dimensionality of our pexels to two (height and regularity), producing a situation that is no better than when regularity was difficult to identify.
Although increasing target patch size or pexel density can make variation in regularity more salient, both methods involve tradeoffs in terms of the kinds of datasets we can visualize, or in the number of attributes our pexels can encode. Because of this, we normally display an attribute with low importance using regularity. While differences in regularity cannot be detected consistently by the low-level visual system, in many cases users will be able to see changes in regularity when areas of interest in a dataset are identified and analyzed in a focused or attentive fashion.
The names "typhoon" and "hurricane" are region-specific, and refer to the same type of weather phenomena: an atmospheric disturbance generally characterized by low pressure, thunderstorm activity, and a cyclic wind pattern. Storms of this type with windspeeds below 17m/s are called "tropical depressions" When windspeeds exceed 17m/s, they become "tropical storms". This is also when storms are assigned a specific name. When windspeeds reach 33m/s, a storm becomes a typhoon (in the Northwest Pacific) or a hurricane (in the Northeast Pacific and North Atlantic).
We combined information from a number of different sources to collect the data we needed. A U.S. Navy elevation dataset was used to obtain land elevations at ten minute latitude and longitude intervals. Land-based weather station readings collected from around the world and archived by the National Climatic Data Center provided daily measurements for eighteen separate environmental conditions. Finally, satellite archives made available by the Global Hydrology and Climate Center contained daily open-ocean windspeed measurements at thirty minute latitude and longitude intervals. The National Climatic Data Center defined the 1997 typhoon season to run from August 1 to October 31; each of our datasets contained measurements for this time period.
We chose to visualize three environmental conditions related to typhoons: windspeed, pressure, and precipitation. All three values were measured on a daily basis at each land-based weather station, but only daily windspeeds were available for open-ocean positions. In spite of the missing open-ocean pressure and precipitation, we were able to track storms as they moved across the Northwest Pacific Ocean. When the storms made landfall the associated windspeed, sea-level pressure, and precipitation were provided by weather stations along their path.
Based on our experimental results, we chose to represent windspeed, pressure, and precipitation with height, density, and regularity, respectively. Localized areas of high windspeed are an obvious indicator of storm activity. We chose to map increasing windspeed to an increased pexel height. Our experimental results showed that taller pexels can be identified preattentively, regardless of any background texture pattern which might be present. Windspeed has two important boundaries: 17m/s (where tropical depressions become tropical storms) and 33m/s (where storms become typhoons). We mirrored these boundaries with height discontinuities. Pexel height increases linearly from 0-17m/s. At 17m/s, height approximately doubles, then continues linearly from 17-33m/s. At 33m/s another height discontinuity is introduced, followed by a linear increase for any windspeeds over 33m/s.
Pressure is represented with pexel density. An increase in pressure is mapped to a decrease in pexel density (i.e., very dense pexels represent areas of very low pressure). Pressure below 996 millibars produces very dense pexels. Pressure between 996 and 1014 millibars is represented by dense pexels. Pressure over 1014 millibars results in sparse pexels. Our experimental results showed it was easier to find dense pexels in a sea of sparse pexels, as opposed to sparse in dense. Our mapping uses high-density pexels to highlight the low-pressure areas associated with typhoon activity.
Precipitation is represented with pexel regularity. High levels of precipitation result in an irregular pexel pattern. Pexel positions are held regular for a daily rainfall of 0.13 inches or less (the median value for the time period we visualized). Daily rainfall over 0.13 inches produces an increased pexel irregularity. Because precipitation was not as important as either windspeed or pressure during visualization, it was assigned to our least effective texture dimension, regularity.
 (a) |
|
 (b) |
 (c) |
 (d) |
 (e) |





Click on any image to view the corresponding movie (f) |
|





Click on any image to view the corresponding movie (g) |
|
Figure 6: (a) Weather conditions for Japan and Korea, and windspeeds for the surrounding open ocean (August 1, 1997); (b) windspeed mapped to height, pressure mapped to density, precipitation mapped to regularity: looking south, typhoon Amber moves east to west across the Northwest Pacific (August 26, 1997); (c) typhoon Amber makes landfall on the island of Taiwan (August 28, 1997); (d, e) same data as for (b) and (c), but with windspeed mapped to regularity, pressure mapped to height, precipitation mapped to density: the use of regularity makes it significantly more difficult to track typhoons when they make landfall; (f) a movie of tropical storm Victor, typhoon Winnie, and typhoon Amber moving through the east Asia region; (g) a movie of hurricane Fran moving through the U.S. east coast
We built a simple visualization tool that maps windspeed, pressure, and precipitation to their corresponding height, density, and regularity. Our visualization tool allows a user to move forwards and backwards through the dataset day-by-day. One interesting result was immediately evident when we began our analysis: typhoon activity was not represented by high windspeed values in our open-ocean dataset. Typhoons normally contain severe rain and thunderstorms. The high levels of cloud-based water vapor produced by these storms block the satellites that are used to measure open-ocean windspeeds. The result is an absence of any windspeed values within a typhoon's spatial extent. Rather than appearing as a local region of high windspeeds, typhoons on the open-ocean are displayed as a "hole", an ocean region without any windspeed readings (see Figure 6b and Figure 6d). This absence of a visual feature (i.e., a hole in the texture field) is large enough to be salient in our displays, and can be preattentively identified and tracked over time. Therefore, users have little difficulty finding storms and watching them as they move across the open ocean. When a storm makes landfall, the weather stations along the storm's path provide the proper windspeed, as well as pressure and precipitation. Weather stations measure windspeed directly, rather than using satellite images, so high levels of cloud-based water vapor cause no loss of information.
Figure 6 shows windspeed, pressure, and precipitation around Japan, Korea, and Taiwan during August, 1997. Figure 6a looks north, and displays normal summer conditions across Japan on August 1, 1997. Figure 6b, looking south, tracks typhoon Amber (one of the region's major typhoons) approaching along an east to west path across the Northwest Pacific Ocean on August 26, 1997. Figure 6c shows typhoon Amber two days later as it moves through Taiwan. Weather stations within the typhoon show the expected strong winds, low pressure, and high levels of rainfall. These results are easily identified as tall, dense, irregular pexels. Compare these images to Figures 6d-e, where windspeed was mapped to regularity, pressure to height, and precipitation to density (a mapping that our experiments predict will perform poorly). Although viewers can identify areas of lower and higher windspeed (e.g., on the open ocean and over Taiwan), it is difficult to identify a change in lower or higher windspeeds (e.g., the change in windspeed as typhoon Amber moves onshore over Taiwan). In fact, viewers often searched for an increase in height that represents a decrease in pressure, rather than an increase in irregularity; pexels over Taiwan become noticeably taller between Figures 6d and 6e.
Clearly, we would like to combine our pexels with other visual features like orientation, color, intensity, motion, and isocontours. For example, Healey [Hea96c] describes a method for selecting perceptually balanced colors. This technique was used along with height and density to display cultivation data in North and Central America (Figure 1b). As with our texture dimensions, we need to consider visual interference and feature preference when colored pexels are displayed. We are also interested in using orientation to encode additional data attributes. Since our pexels are three-dimensional, they can be oriented in various ways. We are designing experiments to investigate the effectiveness of orientation for encoding information, and the interactions that occur when multiple texture and color dimensions are displayed simultaneously.
Although our example application was the visualization of environmental conditions on topographical maps, our techniques are not restricted to only these types of datasets. We are currently investigating the use of pexels to visualize the rigid and rotational velocities on the surface of a three-dimensional object as it moves over time. Spatially coherent regions of pexels with a common appearance correspond to parts of an object with common rigid and rotational velocities. We hope that the ability to visually identifying these regions will help us perform rigid-body segmentation. Another possible application is the use of pexels to represent information during the visualization of medical scans (e.g., CT or MRI). A reconstructed medical volume is normally made up of multiple surfaces representing different materials (i.e., bone, blood vessels, and muscle) embedded within the volume. Transparency and cutting planes can be used to show the interior of the volume. We are investigating methods for encoding additional information on each material's surface through the use of pexels. For this environment, our pexels are two-dimensional (i.e., oriented discs, lines, or other two-dimensional shapes) and lie flat on each surface. We are hoping to build pexels that display information to the user without masking the underlying surface's shape, orientation, and position within the volume.
| [Aks96] | Aks, D. J. and Enns, J. T. Visual search for size is influenced by a background texture gradient. Journal of Experimental Psychology: Perception and Performance 22, 6 (1996), 1467-1481. |
| [Gri89] | Grinstein, G., Pickett, R., and Williams, M. EXVIS: An exploratory data visualization environment. In Proceedings Graphics Interface '89 (London, Canada, 1989), pp. 254-261. |
| [Hal92] | Hallett, P. E. Segregation of mesh-derived textures evaluated by resistance to added disorder. Vision Research 32, 10 (1992), 1899-1911. |
| [Har73] | Haralick, R. M., Shanmugam, K., and Dinstein, I. Textural features for image classification. IEEE Transactions on System, Man, and Cybernetics SMC-3, 6 (1973), 610-621. |
| [Hea96a] | Healey, C. G., Booth, K. S. and Enns, J. T. High-speed visual estimation using preattentive processing. ACM Transactions on Computer Human Interaction 3, 2 (1996), 107-135. |
| [Hea96c] | Healey, C. G. Choosing effective colours for data visualization. In Proceedings Visualization '96 (San Francisco, California, 1996), pp. 263-270. |
| [Int97] | Interrante, V. Illustrating surface shape in volume data via principle direction-driven 3D line integral convolution. In SIGGRAPH 97 Conference Proceedings (Los Angeles, California, 1997), T. Whitted, Ed., pp. 109-116. |
| [Jul81b] | Juléesz, B. A theory of preattentive texture discrimination based on first-order statistics of textons. Biological Cybernetics 41 (1981), 131-138. |
| [Jul84] | Juléesz, B. A brief outline of the texton theory of human vision. Trends in Neuroscience 7, 2, (1984), 41-45. |
| [Liu94] | Liu, F. and Picard, R. W. Periodicity, directionality, and randomness: Wold features for perceptual pattern recognition. In Proceedings 12th International Conference on Pattern Recognition (Jerusalem, Israel, 1994), pp. 1-5. |
| [Mal90] | Malik, J. and Perona, P. Preattentive texture discrimination with early vision mechanisms. Journal of the Optical Society of America A 7, 5 (1990), 923-932. |
| [Rao93a] | Rao, A. and Lohse, G. L. Towards a texture naming system: Identifying relevant dimensions of texture. In Proceedings Visualization '93 (San Jose, California, 1993), pp. 220-227. |
| [Rao93b] | Rao, A. R. and Lohse, G. L. Identifying high level features of texture perception. CVGIP: Graphics Models and Image Processing 55, 3 (1993), 218-233. |
| [Ree93] | Reed, T. R. and Hans Du Buf, J. M. A review of recent texture segmentation and feature extraction techniques. CVGIP: Image Understanding 57, 3 (1993), 359-372. |
| [Sal97] | Salisbury, M., Wong, M. T., Hughes, J. F., and Salesin, D. H. Orientable textures for image-based pen-and-ink illustration. In SIGGRAPH 97 Conference Proceedings (Los Angeles, California, 1997). T. Whitted, Ed., pp. 401-406. |
| [Sch83] | Schweitzer, D. Artificial texturing: An aid to surface visualization. Computer Graphics (SIGGRAPH 83 Conference Proceedings) 17, 3 (1983), 23-29. |
| [Tam78] | Tamura, H., Mori, S., and Yamawaki, T. Textural features corresponding to visual perception. IEEE Transactions on Systems, Man, and Cybernetics SMC-8, 6 (1978), 460-473. |
| [Tri85] | Triesman, A. Preattentive processing in vision. Computer Vision, Graphics, and Image Processing 31 (1985), 156-177. |
| [Tur96] | Turk, G. and Banks, D. Image-guided streamline placement. In SIGGRAPH 96 Conference Proceedings (New Orleans, Louisiana, 1996), H. Rushmeier, Ed., pp. 453-460. |
| [War92] | Ware, C. and Knight, W. Orderable dimensions of visual texture for data display: Orientation, size, and contrast. In Proceedings SIGCHI '92 (Monterey, California, 1992), pp. 203-209. |
| [War95] | Ware, C. and Knight, W. Using visual texture for information display. ACM Transactions on Graphics 14, 1 (1995), 3-20. |
| [Win96] | Winkenbach, G. and Salesin, D. H. Rendering freeform surfaces in pen-and-ink. In SIGGRAPH 96 Conference Proceedings (New Orleans, Louisiana, 1996), H. Rushmeier, Ed., pp. 469-476. |
| [Wol94] | Wolfe, J. M. Guided Search 2.0: A revised model of visual search. Psychonomic Bulletin & Review 1, 2 (1994), 202-238. |