
This module offers a brief foundation to the basics of linear algebra. We will focus on topics relevant to upcoming data science techniques, which include vectors, matrices, linear equation solving, eigenvectors and eigenvalues, projections, and least squares. In spite of our limited focus, this covers much of what would be included in a first-year algebra course, highlighting that even the fundamentals of an important mathematical area like linear algebra are broad and rigorous.
So, what is linear algebra? Yes, it is a required course you probably took in high school or during your undergraduate degree. But more than that, it is a fundamental foundation to most areas in mathematics. For example, matrix factorization, which is part of linear algebra, is used to convert raw text into semantic concepts for text document clustering. Linear algebra also acts as a foundation to the computer graphics used in modern video games. Because of this, it is critical that you have a strong understanding of the basics of linear algebra as it pertains to the data science topics we will cover.
In terms of the technical definition of linear algebra, it is an area of mathematics that focuses on linear equations and their representations as vectors and matrices. One common linear equation, and one I'm sure you'll recognize, is the slope–intercept form \(y = mx + b,\) a line with slope \(m\) and \(y\)-axis intercept \(b\) in 2D. A concrete example would be \(y = 3x + 1.\) Here, a unit increase in \(x\) produces a three unit increase in \(y\) (slope \(m=3,\)) and when \(x=0,\) \(y=1\) (the line intercepts the \(y\)-axis at \(b=1.\)) Parametric equations are used for line segments \(c_1 \leq t \leq c_2\), for example, \(c_1 = 0\), \(c_2 = 1\) defines the line segment from \((0,1)\) to \((1,4\)).
Other representations exist, each with their own advantages. For example, the parametric representation of a 2D line is \(p(t) = (f_1(t),f_2(t)),\) where functions \(f_1\) and \(f_2\) define values for \(x\) and \(y\) in terms of parametric parameter \(t.\) The concrete example \(p(t) = (t,3t+1)\) is equivalent to \(y=3x+1,\) since it produces the same set of points forming the same line in 2D.
Two advantages of a parametric representation versus the slope–intercept form are:
Much of first year linear algebra focuses on different ways to solve systems of linear equations, usually written in matrix–vector form \(Ax = b.\) Given an \(m\) row by \(n\) column matrix \(A\) and an \(n\) element vector \(b\), what values of the \(m\) element vector \(x\) satisfy this equation? Although solving systems of linear equations is used in data science, a more important take-away is the mechanics it teaches. Understanding how systems of linear equations are solved builds the foundation we need for more relevant operations like principal component analysis or minimizing least squares.
My experience is that a critical requirement to understanding any topic, and in particular theoretical topics, is to understand the vocabulary or terminology of the topic. Without this understanding, many statements will seem nonsensical. For example, consider the following statement in the linear algebra domain.
If you don't know what orthonormal means, this sounds like some sort of unintelligible foreign language. However, if I tell you that: (1) orthonormal vectors are orthogonal to one another and normalized; (2) if two vectors are orthogonal it means they are perpendicular to one another, that is, they form a 90° right angle where they meet; and (3) if a vector is normalized, it means its length is 1 (we will define a vector's length in the next section.) Now, the idea of orthonormality should make more sense. Notice also that the definition of one term may involve other terms (orthonormal involves both orthogonal and normalization), so you need to understand the meaning of the term and all its subterms to fully understand what it represents.
Throughout these notes I will try to define any linear algebra term that I think may be uncommon and important to our discussions. I strongly encourage you to commit these definitions to memory, so when you read explanations of different linear algebra theory and algorithms, you can quickly convert descriptions in linear algebra terminology to concrete, practical descriptions that are simple to understand.
A common confusion when initially studying linear algebra is, "What is the difference between a point and a vector?" On a 2D plane, both are a two-valued \((x,y)\) element. The main difference is not in how they are represented, but what they represent. A point \(p = (x,y)\) is a fixed position in 2D space. A vector \(\vec{v} = [v_1,v_2]\) is a direction and a length from some user-chosen position or point.
Consider a concrete example \(p=(1,2)\) and \(\vec{v}=[2,4].\) Anchoring \(\vec{v}\) at \(p\) says we want to create a line segment starting at \((1,2),\) and moving 2 units in the \(x\)-direction and 4 units in the \(y\)-direction to an ending position \((3,6).\) That is, \(\vec{v}\) defines a direction to move, and a distance to move in the given direction. If we changed \(p,\) we would get a line segment with different starting and ending positions, but it would have exactly the same direction and length. That is, it would be exactly the same line segment, just shifted to some other position on the 2D plane.
Vectors are an ordered list of numbers in either row (horizontal) orientation \(\vec{v} = [ v_1, \ldots, v_n ]\) or column (vertical) orientation \(\vec{v} = \begin{bmatrix} v_1 \\ \ldots \\ v_n \end{bmatrix}.\) Vectors are represented in the notes as an italic letter with an arrow above it. One vector that is sometimes identified explicitly is the zero vector, a vector whose entries are all zero, \(\mathbf{\vec{0}} = [ 0, \ldots, 0 ].\)
The linear combination of two vectors \(\vec{u}\) and \(\vec{v}\) adds the vectors, possibly with a scalar multiplication of one or both of the vectors by constant values \(c\) and \(d.\) \begin{equation} c \vec{u} + d \vec{v} \label{eq:lin-comb} \end{equation}
Practical Example. Consider \(c=2,\) \(d=-3,\) \(\vec{u} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -1 \\ 2 \end{bmatrix}.\) \begin{equation} c\vec{u} + d\vec{v} = 2 \begin{bmatrix} 3 \\ 4 \end{bmatrix} - 3 \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 6 \\ 8 \end{bmatrix} + \begin{bmatrix} 3 \\ -6 \end{bmatrix} = \begin{bmatrix} 9 \\ 2 \end{bmatrix} \end{equation}
The dot product or inner product of two vectors \(\vec{u} = \begin{bmatrix} u_1 & \cdots & u_n \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix}\) is written as \(\vec{u} \cdot \vec{v}.\) The dot product takes corresponding entries from \(\vec{u}\) and \(\vec{v},\) multiples them, and sums them \(\sum_{i=1}^{n}u_i v_i\) to produce a single scalar value. \begin{equation} \vec{u} \cdot \vec{v} = \begin{bmatrix} u_1 & \cdot & u_n \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix} = \sum_{i=1}^{n} u_i v_i \end{equation}
Practical Example. Consider \(\vec{u} = \begin{bmatrix} 1 & 2 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} 4 \\ 5 \end{bmatrix}.\) \begin{equation} \vec{u} \cdot \vec{v} = \begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 4 \\ 5 \end{bmatrix} = (1)(4) + (2)(5) = 14 \end{equation}
Both Python and R have built-in dot product functions.
Two vectors \(\vec{u} = \begin{bmatrix} u_1 & \cdots & u_n \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix}\) are orthogonal when they are perpendicular to one another, forming a 90° right angle where they meet. This occurs when the dot product between the two vectors is zero.
Practical Example. Consider \(\vec{u} = \begin{bmatrix} 4 & 2 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -1 \\ 2 \end{bmatrix}.\) \begin{equation} \vec{u} \cdot \vec{v} = \begin{bmatrix} 4 & 2 \end{bmatrix} \cdot \begin{bmatrix} -1 \\ 2 \end{bmatrix} = (4)(-1) + (2)(2) = 0 \end{equation}
The graph below demonstrates this visually using an anchor point for both vectors of \(p=(1,1).\)
The length of a vector is related to its dot product. Specifically, the length of vector \(\vec{v}\) is \(\left\lVert \vec{v} \right\rVert = \sqrt{\vec{v} \cdot \vec{v}}\;\;\) (the hypotenuse of a right angle triangle with sides \((0,0)\)–\((x,0)\) and \((x,0)\)–\((x,y))\)
Practical Example. Consider \(\vec{v}\ = \begin{bmatrix} 4 \\ 5 \end{bmatrix}\) from the dot product example. \begin{equation} \left\lVert \vec{v} \right\rVert = \sqrt{\begin{bmatrix} 4 & 5 \end{bmatrix} \cdot \begin{bmatrix} 4 \\ 5 \end{bmatrix}} = \sqrt{(4)(4) + (5)(5)} = \sqrt{41} = 6.4 \end{equation}
Python has a built-in vector length function norm. In R,
you can geometry's dot() function or the
built-in %*% operator, that performs vector dot product
or full matrix multiplication.
An important class of vectors are unit vectors. A vector is unit if its length is 1, that is, \(\left\lVert \vec{v} \right\rVert = 1.\) Any \(\vec{v}\) can be converted to a unit vector or normalized by dividing its entries by \(\left\lVert \vec{v} \right\rVert.\)
Practical Example. Consider \(\vec{v} = \begin{bmatrix} 4 \\ 5 \end{bmatrix}\) above. We know \(\left\lVert \vec{v} \right\rVert = 6.4,\) so dividing \(\vec{v}\) by its length gives us a new vector \(\vec{v^{\prime}} = \frac{1}{6.4} \begin{bmatrix} 4 \\ 5 \end{bmatrix} = \begin{bmatrix} 0.625 \\ 0.781 \end{bmatrix}.\) To confirm \(\vec{v^{\prime}}\) is unit, we compute its length \(\left\lVert \vec{v^{\prime}} \right\rVert.\) \begin{equation} \left\lVert \vec{v^{\prime}} \right\rVert = \sqrt{ 0.625^{2} + 0.781^{2} } = \sqrt{ 0.40 + 0.60 } = \sqrt{ 1.0 } = 1.0 \end{equation}
Notice also that, importantly, \(\vec{v}\) and \(\vec{v^{\prime}}\) both point in the same direction. The only difference is in their lengths.
The angle \(\theta\) between two vectors \(\vec{u}\) and \(\vec{v}\) is defined as \(\displaystyle \cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{\left\lVert \vec{u} \right\rVert \left\lVert \vec{v} \right\rVert}.\) We can use the \(\arccos(\theta)\) function to obtain the value of \(\theta\) if necessary. Notice also that if \(\vec{u}\) and \(\vec{v}\) have been normalized to be unit vectors, the formula simplifies to dot product of the two vectors, \(\cos(\theta) = \vec{u} \cdot \vec{v}.\)
Practical Example. Consider \(\vec{u} = \begin{bmatrix} 0 & 1 \end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} 2 \\ 2 \end{bmatrix}.\) Given an anchor point \(p=(1,1),\) the vectors can be visualized on a 2D plane.
Computing \(\vec{u} \cdot \vec{v},\) \(\left\lVert \vec{u} \right\rVert,\) and \(\left\lVert \vec{v} \right\rVert\) allows us to determine the angle between \(\vec{u}\) and \(\vec{v}.\) \begin{align} \begin{split} \vec{u} \cdot \vec{v} &= (0)(2) + (1)(2) = 2\\ \left\lVert \vec{u} \right\rVert &= \sqrt{0^2 + 1^2} = 1\\ \left\lVert \vec{v} \right\rVert &= \sqrt{2^2 + 2^2} = 2.8284\\ \cos(\theta) &= \frac{2}{(1)(2.8284)} = 0.7071\\ \theta &= \arccos(0.7071) = 45^\circ\\ \end{split} \end{align}
If we take a theoretical aside, remember that \(\cos(\theta)\) never exceeds one, since its range is \([-1, 1].\) Combining this with the formula for the angle between vectors gives us two famous inequalities: the Schwarz inequality and the triangle inequality.
| Schwarz Inequality: |
\(\left\lvert \vec{u} \cdot \vec{v} \right\rvert \leq \left\lVert \vec{u} \right\rVert \left\lVert \vec{v} \right\rVert\) |
| Triangle Inequality: |
\(\left\lVert \vec{u} + \vec{v} \right\rVert \leq \left\lVert \vec{u} \right\rVert + \left\lVert \vec{v} \right\rVert\) |
Although these aren't necessarily critical for our data science discussions, they are two of the most famous formulas in mathematics, so if you wondered where they came from or how to prove them, this is one possible approach.
A matrix is a rectangular combination of values arranged as \(m\) rows and \(n\) columns. The size of a matrix is row major, so a \(3 \times 2\) matrix \(A\) has \(m=3\) rows and \(n=2\) columns \(A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}.\)
Transpose swaps rows and columns, where rows from top-to-bottom become columns from left-to-right. A transposed row vector is a column vector, and a transposed column vector is a row vector. A transposed matrix \(A^{T}\) converts the rows of \(A\) to columns and the columns of \(A\) to rows, that is, \(a_{ij} \in A = a_{ji} \in A^{T}.\) Four useful properties of transpose are often applied.
\begin{align} \begin{split} A = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 0 \end{bmatrix} & \quad \Rightarrow \quad A^{T} = \begin{bmatrix} 1 & -1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{bmatrix}\\[8pt] \begin{bmatrix} \quad\quad R_1 \quad\quad \\ \quad\quad R_2 \quad\quad \\ \quad\quad \vdots \quad\quad \\ \quad\quad R_n \quad\quad \\ \end{bmatrix} & \quad \Rightarrow \quad \begin{bmatrix} \\ R_1^{T} & R_2^{T} & \cdots & R_n^{T}\\ \\ \end{bmatrix} \end{split} \end{align}
Consider a \(3 \times 3\) matrix \(A = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}.\) The linear combination of \(A\) with a column vector \(\vec{x} = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}^{T}\) produces a resulting column matrix of the same height as \(A.\) One way to approach this problem is known as combination of columns. If we divide \(A\) into three column vectors \(A_{\ast 1} = \begin{bmatrix}1 & -1 & 0 \end{bmatrix}^{T}\) \(A_{\ast 2} = \begin{bmatrix}0 & 1 & -1 \end{bmatrix}^{T},\) and \(A_{\ast 3} = \begin{bmatrix}0 & 0 & 1 \end{bmatrix}^{T},\) then we can combine individual elements of \(\vec{x}\) with \(A_{\ast 1},\) \(A_{\ast 2},\) and \(A_{\ast 3}\) to generate the linear combination. \begin{equation} \label{eq:vec_mult} x_1 \begin{bmatrix} 1 \\ -1 \\ 0 \end{bmatrix} + x_2 \begin{bmatrix} 0 \\ 1 \\ -1 \end{bmatrix} + x_3 \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 - x_1 \\ x_3 - x_2 \end{bmatrix} \end{equation}
Notice that combination of columns is different that the traditional approach of row combination where we take each row of \(A,\) for example \(A_{1 \ast} = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\) and multiply it by \(\vec{x}\) to produce the first element of the linear combination vector \(x_1.\) Based on our discussion of vectors, what actually happens is each entry of the resulting vector is the dot product of the corresponding row of \(A\) with \(\vec{x}.\) \begin{equation} A\vec{x} = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}^{T} \\ \begin{bmatrix} -1 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}^{T} \\ \begin{bmatrix} 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}^{T} \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 - x_1 \\ x_3 - x_2 \end{bmatrix} \end{equation}
Another important point shown above is that we normally do not divide \(A\) into individual row vectors. Instead we perform matrix–vector multiplication \(A\vec{x}\) to generate the linear combination vector \(\vec{b}.\) \begin{equation} \label{eq:mat_mult} A\vec{x} = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 - x_1 \\ x_3 - x_2 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \vec{b} \end{equation}
Conceptually, there is a difference between Eqns \eqref{eq:vec_mult} and \eqref{eq:mat_mult}. In Eqn \eqref{eq:vec_mult}, \(x_1,\) \(x_2,\) and \(x_3\) multiply the column vectors of \(A.\) In Eqn \eqref{eq:mat_mult}, \(A\) is acting on the column vector \(\vec{x}.\) The output \(A\vec{x}\) is a combination \(\vec{b}\) of the columns of \(A.\)
Our examples to this point provide known values for \(A\) and \(\vec{x},\) allowing us to calculate \(\vec{b}.\) In a linear equation, we are given values for \(A\) and \(\vec{b},\) and asked to calculate an \(\vec{x}\) that multiplies with \(A\) to produce the desired \(\vec{b}.\) This is the inverse problem, so named because the inverse of \(A,\) denoted \(A^{-1},\) can be used to calculate the required \(\vec{x},\) \(\vec{x} = A^{-1}\vec{b}.\)
Consider Eqn \eqref{eq:mat_mult}. Here we know \(x_1 = b_1,\) so for the second element \(x_2 - x_1 = b_2\) we can substitute \(x_1 = b_1\) to produce \(x_2 = b_1 + b_2.\) Finally, we use the same approach on the third element to produce \(x_3 = b_1 + b_2 + b_3.\) Now, given values for \(\vec{b},\) we can directly calculate \(\vec{x}.\) Obviously, this is a very simple example. We did not need to derive \(A^{-1}\) to solve for \(\vec{x}.\) Notice, however, that since we know \(\vec{x} = A^{-1}\vec{b}\) and we've determine how to generate each \(x_i\) from \(\vec{b},\) we have indirectly solved for \(A^{-1}.\) \begin{equation} \begin{split} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} b_1 \\ b_1 + b_2 \\ b_1 + b_2 + b_3 \end{bmatrix} &= \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = A^{-1} \vec{b}\\ \therefore \;\; A^{-1} &= \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix} \end{split} \end{equation}
We will talk in more detail about the inverse matrix below, including examples to solve the matrix both mathematically and programatically. At this point, you can think intuitively of \(A^{-1}\) as canceling \(A\) in a matrix equation.
To begin, recall that a matrix is an \(m \times n\) rectangular collection of numbers made up of \(m\) rows and \(n\) columns. Individual entries in a matrix \(A\) are denoted \(a_{ij}\) for the entry in row \(i\) and column \(j.\) Row \(i\) of \(A\) is written as \(A_{i \ast}\) and column \(j\) of \(A\) is written as \(A_{\ast j}.\) \begin{align} A &= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \end{align}
Matrices \(A\) and \(B\) with the same shape can be added \(C = A + B\) by combining corresponding entries \(c_{ij} = a_{ij} + b_{ij}.\) A matrix \(A\) can be multiplied by a constant value \(s,\) \(C = s A\) by multiplying each entry in \(A\) by \(s,\) \(c_{ij} = s\,a_{ij}.\) It is also important to understand that matrix multiplication is associative and distributive, but it is normally not commutative.
| Associative: |
\(A(BC) = (AB)C\) |
| Left Distributive: |
\(A(B+C) = AB + AC\) |
| Right Distributive: |
\((A+B) C = AC + BC\) |
| Commutative: |
\(AB \neq BA\) (except in special cases) |
In order to multiple two matrices \(A\) and \(B,\) the number of columns in \(A\) MUST be identical to the number of rows in \(B.\) \begin{align} \label{eq:mat_mult_ex} \begin{split} \begin{bmatrix} \; \\ \;m \times n\; \\ \; \end{bmatrix} \begin{bmatrix} \; \\ \;n \times p\; \\ \; \end{bmatrix} &= \begin{bmatrix} \; \\ \;m \times p\; \\ \; \end{bmatrix}\\[24pt] \begin{bmatrix} 2 & 3 \\ 4 & 5 \\ 6 & 7 \\ 8 & 9 \end{bmatrix} \begin{bmatrix} 1 & 1 & 2 \\ 3 & 5 & 8 \end{bmatrix} &= \begin{bmatrix} 11 & 17 & 28 \\ 19 & 29 & 48 \\ 27 & 41 & 68 \\ 35 & 53 & 88 \end{bmatrix}\\[8pt] \begin{bmatrix}m=4 \times n=2\end{bmatrix} \begin{bmatrix}n=2 \times p=3\end{bmatrix} &= \begin{bmatrix}m=4 \times p=3\end{bmatrix} \end{split} \end{align}
So, the shape of \(A\) and \(B\) determine the shape of \(C = AB.\) But what do we actually do to calculate the entries \(c_{ij} \in C\)?
There are numerous ways to explain how to multiply matrices. We will start with the most common method, which involves taking the dot product of row \(i\) of \(A\) and column \(j\) of \(B\) to calculate \(c_{ij}.\) \begin{align} \begin{array}{c c c c} \begin{bmatrix} \ast \\ a_{i1} & a_{i2} & \cdots & a_{i5} \\ \ast \\ \ast \\ \end{bmatrix} & \begin{bmatrix} \ast & \ast & b_{1j} & \ast & \ast & \ast \\ & & b_{2j} \\ & & \vdots \\ & & b_{5j} \end{bmatrix} & = & \begin{bmatrix} & & \ast \\ \ast & \ast & c_{ij} & \ast & \ast & \ast\\ & & \ast \\ & & \ast \\ \end{bmatrix}\\[8pt] A: [4 \times 5] & B: [5 \times 6] & = & C: (4 \times 5) \; (5 \times 6) = 4 \times 6 \end{array} \end{align}
Here \(i=2\) and \(j=3,\) so \(c_{23}\) is \(A_{2 \ast} \cdot B_{\ast 3}.\)
Practical Example. Consider the matrices in Eqn \eqref{eq:mat_mult_ex}. \begin{equation} c_{23} = A_{2 \ast} B_{\ast 3} = \begin{pmatrix} 4 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 8 \end{pmatrix} = (4)(2) + (5)(8) = 48. \end{equation}
And indeed, \(c_{23}\) in Eqn \eqref{eq:mat_mult_ex} is \(48.\) Exactly the same approach is used to calculate \(c_{ij} \; \forall \, i,j.\)
Another way of looking at matrix multiplication is through a column perspective. \(A\) is multiplied against each column in \(B\) to produce a corresponding column in \(C.\)
\begin{align*} \begin{split} A \begin{bmatrix} B_{\ast j} \end{bmatrix} &= \begin{bmatrix} C_{\ast j} \end{bmatrix}^{T} \end{split} \end{align*}Practical Example. Calculate \(C_{\ast 3}\) in Eqn \eqref{eq:mat_mult_ex}. \begin{equation} C_{\ast 3} = A B_{\ast 3} = \begin{bmatrix} 2 & 3 \\ 4 & 5 \\ 6 & 7 \\ 8 & 9 \end{bmatrix} \begin{bmatrix} 2 \\ 8 \end{bmatrix} = \begin{bmatrix} 28 & 48 & 68 & 88\end{bmatrix}^{T} \end{equation}
The result corresponds to \(C_{\ast 3}^{T}\) as expected. If we apply this approach \(\forall \, j\) will will generate all \(C_{\ast j} \in C.\)
Not surprisingly, you can take a row perspective as well, if you prefer. Here, we multiple rows \(A_{i \ast}\) of \(A\) against \(B\) to produce rows \(C_{i \ast}.\)
Practical Example. Calculate \(C_{2 \ast}\) in Eqn \eqref{eq:mat_mult_ex}. \begin{equation} C_{2 \ast} = A_{2 \ast} B = \begin{bmatrix} 4 & 5 \end{bmatrix} \begin{bmatrix} 1 & 1 & 2 \\ 3 & 5 & 8 \end{bmatrix} = \begin{bmatrix} 19 & 29 & 48 \end{bmatrix} \end{equation}
This corresponds to \(C_{2 \ast}\) as expected.
Both Python and R support matrix multiplication. Python does this with
the matmul function (or more recently with
the @ operator). You can create numpy arrays and multiply
them with matmul (assuming they satisfy the shape
constraints described above) to obtain results. In R, the operator
%*% performs matrix multiplication. One important
difference between Python and R is that Python defines its matrices in
a row major fashion, that is, row by row, where R defines its
matrices column by column using a column major
approach. Consider the matrices \(A = \begin{bmatrix} 1 & 2 & 3 \\ 4 &
5 & 6 \\ 7 & 8 & 9 \end{bmatrix},\) \(B = \begin{bmatrix} 1 & 1 & 2 \\
3 & 5 & 8 \\ 13 & 21 & 34 \end{bmatrix},\) and \(\vec{v} =
\begin{bmatrix} 10 \\ 11 \\ 12 \end{bmatrix}.\)
The identity matrix \(I\) is a special matrix with the following properties.
\begin{equation} A I_2 = \begin{bmatrix} 2 & 3 \\ 4 & -1 \\ 0 & 5 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} (2)(1) + (3)(0) & (2)(0) + (3)(1) \\ (4)(1) + (-1)(0) & (4)(0) + (-1)(1) \\ (0)(1) + (5)(0) & (0)(0) + (5)(1) \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 4 & -1 \\ 0 & 5 \end{bmatrix} = A \end{equation} \begin{equation} I_3 A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 3 \\ 4 & -1 \\ 0 & 5 \end{bmatrix} = \begin{bmatrix} (1)(2) + (0)(4) + (0)(0) & (1)(3) + (0)(-1) + (0)(5) \\ (0)(0) + (1)(4) + (0)(0) & (0)(3) + (1)(-1) + (0)(5) \\ (0)(0) + (0)(4) + (1)(0) & (0)(3) + (0)(-1) + (1)(5) \\ \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 4 & -1 \\ 0 & 5 \end{bmatrix} = A \end{equation}
Both Python and R have built-in functions to create identity matrices of a user-chosen size.
Given a matrix \(A,\) its inverse is denoted \(A^{-1}.\) You can think of \(A^{-1}\) as the reciprocal of \(A.\) For numbers, the reciprocal of \(n\) is \(\frac{1}{n}.\) For example, the reciprocal of 8 is \(\frac{1}{8}.\) The reciprocal has the property that a number multiplied by its reciprocal equals one, \((8) (\frac{1}{8}) = 1.\) There is no notion of division for matrices, however, the inverse acts similarly to reciprocals for numbers. A matrix \(A\) multiplied by its inverse \(A^{-1}\) produces the identity matrix \(I,\) \(A A^{-1} = A^{-1} A = I,\) which can be seen as the matrix equivalent of the number 1.
What is the purpose of \(A^{-1}?\) The inverse matrix has many important functions, but consider a simple case. Suppose I have the formula \(A \vec{x} = \vec{b}\) and I know the values for \(A\) and \(\vec{b},\) but need to solve for \(\vec{x}.\) If these were numbers and not matrices and vectors, I would simply divide through by \(A.\)
\begin{equation*} \vec{x} = \frac{\vec{b}}{A} \end{equation*}As we noted above, however, there is no notion of division for matrices. However, we can perform an operation that produces an identical result using the inverse matrix \(A^{-1}.\)
\begin{equation*} \begin{split} A^{-1} A \vec{x} &= A^{-1} \vec{b} \\ I \vec{x} &= A^{-1} \vec{b} \\ \vec{x} &= A^{-1} \vec{b} \end{split} \end{equation*}So, given \(A,\) how do you calculate \(A^{-1}.\) A simple equation can be used for \(2 \times 2\) matrices, but as the size of the matrix increases, it becomes more difficult to compute its inverse. There are also two important points to state about a matrix's inverse. The first is that (true) inverses only exist for square matrices \(A\) where \(n = m.\) The second is that an inverse may not exist. In this case, \(A\) is called singular or degenerate.
For a \(2 \times 2\) matrix \(A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix},\) we first calculate the determinant of \(A,\) \(\textrm{det}(A) = |A| = a_{11} a_{22} - a_{12} a_{21}.\) If \(|A|=0\) then \(A\) is singular and no inverse exists. Otherwise, \(A^{-1} = \frac{1}{|A|} \begin{bmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{bmatrix}.\) As a practical example, consider \(A = \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix}.\) \begin{equation} \label{eq:det_2x2} \begin{split} |A| &= (4)(6) - (7)(2) = 24 - 14 = 10 \\ A^{-1} &= \frac{1}{10} \begin{bmatrix} 6 & -7 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} 0.6 & -0.7 \\ -0.2 & 0.4 \end{bmatrix} \end{split} \end{equation}
We will discuss determinants to large \(A\) in detail later in the notes. To validate \(A^{-1}\) we compute \(A A^{-1}\) and \(A^{-1} A\) to confirm they both produce \(I_2.\) \begin{equation} \begin{split} A A^{-1} &= \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix} \begin{bmatrix} 0.6 & -0.7 \\ -0.2 & 0.4 \end{bmatrix} \\ &= \begin{bmatrix} (4)(0.6) - (7)(0.2) & -(4)(0.7) + (7)(0.4) \\ (2)(0.6) - (6)(0.2) & -(2)(0.7) + (6)(0.4) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I_2 \\[8pt] A^{-1} A &= \begin{bmatrix} 0.6 & -0.7 \\ -0.2 & 0.4 \end{bmatrix} \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix} \\ &= \begin{bmatrix} (0.6)(4) - (0.7)(2) & (0.6)(7) - (0.7)(6) \\ -(0.2)(4) + (0.4)(2) & -(0.2)(7) + (0.4)(6) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I_2 \\ \end{split} \end{equation}
For larger matrices, methods like Gauss–Jordan or Adjoint–Determinant can be used to identify singular matrices and inverses. In practice, however, we normally use a library in Python or R to return \(A^{-1}\) or identify \(A\) as singular.
Our discussion of computing \(\vec{x}\) for an equation \(A\vec{x} = \vec{b}\) used the inverse \(A^{-1}\) to "simulate" dividing through by matrix \(A.\) Another way of viewing this problem is solving a collection of \(n\) equations with \(n\) unknowns. For example, given \(A = \begin{bmatrix} 1 & -2 \\ 3 & 2 \end{bmatrix},\) \(\vec{b} = \begin{bmatrix} 1 & 11 \end{bmatrix}^{T}\) and \(\vec{x} = \begin{bmatrix} x_1 & x_2 \end{bmatrix}^{T},\) we can rewrite \(Ax = b\) as two equations and two unknowns. \begin{align} \label{eq:two_var_eqn} \begin{split} x_1 -2 x_2 &= 1\\ 3 x_1 + 2 x_2 &= 11 \end{split} \end{align}
The simplest and most well-known way to solve a collection of \(n\) simultaneous equations is through Gaussian elimination. Individual unknowns \(x_1, \ldots\, x_{n-1}\) are successively removed or eliminated from a subset of the equations, eventually producing an equation of the form \(x_n = b_n^{\prime}.\) At this point, we know the value for one of the unknown variables. Because of the way Gaussian elimination works, the remaining equations have two unknowns, three unknowns, up to \(n\) unknowns. We can back-substitute the known \(x_n\) into the equation \(x_{n-1} + x_n = b_{n-1}^{\prime}\) to solve for \(x_{n-1}.\) Now we have known values for two unknowns \(x_n\) and \(x_{n-1}.\) We continue back-substituting to solve for \(x_{n-2},\) \(x_{n-3},\) up to the final unknown \(x_1.\) At this point, we have fully solved for \(\vec{x}.\)
We will use Eqn \eqref{eq:two_var_eqn} as a very simple example of Gaussian elimination. Here, \(n=2,\) the smallest \(n\) we would consider. We require values for \(x_1\) and \(x_2\) where the first equations produces 1 and the second equation produces 11. Visually, we are searching for the intersection of the two lines represented by \(y = \frac{1}{2}x - \frac{1}{2}\) and \(y = -\frac{3}{2} + \frac{11}{2}\) (these are simple rewritings of the two equations in Eqn \eqref{eq:two_var_eqn} to isolate \(y.\))
The lines intersection at \(x_1=3,\) \(x_2=1.\) This is a solution (in fact, the solution) to the system of equations, since \((1)(3) - (2)(1) = 1\) and \((3)(3) + (2)(1) = 11.\) Unfortunately, this type of "visual intersection" becomes significantly more complicated as \(n\) increases. For \(n=3\) we would look for the point where three planes intersect. For \(n > 3\) we begin discussing hyperplanes, which are very difficult to conceptualize visually.
This is why we use Gaussian elimination to solve systems of linear equations of arbitrary size. I'll provide a simple set of steps we apply repeatedly until we isolate a single variable and its corresponding value. Although there is no guarantee this will be possible, for now we will assume no issues arise. Once we understand the basic approach, we will discuss exceptions and what they mean.
Our basic "goal" is to take the original system of equations, and reduce it to an upper-triangular form. \begin{equation} \label{eq:sys_eq_ex} \begin{aligned} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n &= b_1\\ a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n &= b_2\\ \cdots \\ a_{n1} x_1 + a_{n2} x_2 + \cdots + a_{nn} x_n &= b_n \end{aligned} \qquad \Longrightarrow \qquad \begin{aligned} a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n &= b_1 \\ a_{22}^{\prime} x_2 + \cdots + a_{2n}^{\prime} x_n &= b_2^{\prime} \\ \cdots \\ a_{nn}^{\prime} x_n &= b_{n}^{\prime} \end{aligned} \end{equation}
We use some specific terminology to discuss Gaussian elimination. Our first step would be to take the first equation \(eq_1\) and use it to eliminate \(x_1\) from the second equation \(eq_2.\) To do this, we create a new equation \(eq_2^{\prime} = eq_2 - m\,eq_1\). To calculate the multiplier \(m,\) we divide the coefficient \(c\) of \(x_1,\) in \(eq_2\) by the coefficient \(p\) of \(x_1\) in \(eq_1, m = \frac{c}{p}.\) We call \(p\) the pivot.
Practical Example. In Eqn \eqref{eq:sys_eq_ex} pivot \(p=a_{11},\) coefficient \(c=a_{21},\) and multiplier \(m=\frac{a_{21}}{a_{11}}.\)
Once we know \(a_{nn}^{\prime} x_n = b_n^{\prime},\) we back-substitute the (now) known value of \(x_n = \frac{b_{n}^{\prime}}{a_{nn}^{\prime}}\) into the preceding equation \(a_{(n-1)(n-1)}^{\prime} x_{n-1} + a_{nn}^{\prime} x_n = b_{(n-1)}^{\prime}\) to solve for \(x_{n-1}.\) This continues, allowing us to solve for all remaining \(a_{ij}\) and obtain a final solution to the values for every \(x_i.\)
Given our goal of converting \(A \vec{x}\) into an upper-triangular form, we complete the following steps to iteratively work towards the upper-triangular equation set.
Practical Example. Walk through these steps for the linear equations in Eqn \eqref{eq:two_var_eqn}.
We now have a solution to \(A\vec{x} = \vec{b},\) specifically, \(\vec{x} = \begin{bmatrix} 3 & 1 \end{bmatrix}^{T}.\) Substituting these values into the original \(eq_1\) and \(eq_2\) shows that they are correct: \(eq_1: (1)(3) - (2)(1) = 1\) and \(eq_2: (3)(3) + (2)(1) = 11.\) Alternatively, we can solve \(A \vec{x} = \begin{bmatrix} 1 & -2 \\ 3 & 2 \end{bmatrix} \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} (1)(3) + (-2)(1) \\ (3)(3) + (2)(1) \end{bmatrix} = \begin{bmatrix} 1 \\ 11 \end{bmatrix} = \vec{b}.\)
Unfortunately, it is not always possible to obtain a solution to \(Ax = b\) using Gaussian elimination. This should not be surprising, since it is analogous to when the inverse matrix \(A^{-1}\) does not exist. Three types of issues can arise during Gaussian elimination. The first two cannot be corrected. In the third, however, it may be possible to recover by applying row exchange.
No Solutions. The first permanent failure case is one where no solutions exist. Consider the following \(2 \times 2\) system of equations.
If we apply the steps to Gaussian elimination, our multiplier \(m = \frac{3}{1}\) and we replace \(eq_2\) with \(eq_2 - 3 \, eq_1 \rightarrow 0 x_2 = 8.\) Obviously, no value of \(x_2\) can satisfy this equality, so no solution exists for this system of equations. Visually, this corresponds to two parallel lines. Since parallel lines never meet, there is no intersection point to act as a solution.
Infinite Solutions. The second permanent failure case is one where an infinite number of solutions exist. Consider again a \(2 \times 2\) system of equations.
As before, the multiplier \(m = \frac{3}{1} = 3\) and we replace \(eq_2\) with \(eq_2 - 3 \, eq_1 \rightarrow 0 x_2 = 0.\) In this case, any value of \(x_2\) will satisfy the new equation, so we have an infinite choice of possible solutions. Visually, this corresponds to two parallel lines that lie on top of one another, or a second line equation that is a constant multiple of (i.e., that is dependent on) the first.
Row Exchange. A third problem occurs when the pivot \(p=0.\) We cannot compute a multiplier \(m = \frac{c}{p}\) since this produces division by zero. However, if we can find another equation where \(p \neq 0,\) we can swap the two equations and continue with the Gaussian elimination steps.
Here, the pivot in \(eq_1\) is \(p=0.\) To correct this, we exchange \(eq_1\) and \(eq_2.\) Now, \(p=3\) and we can continue with a multiplier of \(m=\frac{0}{3}=0.\) A multiplier of \(m=0\) means we subtract nothing from the (newly exchanged) \(eq_2,\) but this is fine, since \(x_1\) is effectively removed from \(eq_2\) because its coefficient is 0. This results in \(x_2 = 2\) and through back-substitution \(x_1=3,\) which satisfies the original simultaneous linear equations. Note, however, that if there were no other equation with a non-zero \(x_1\) coefficient, there would be no way to perform row exchange to correct our problem and no solution could be found.
Rather than performing equation subtraction, we can eliminate variables from a system of equations using elimination matrices. These matrices are a modified identity matrix, and use exactly the same multiplier we defined previously to perform elimination of one variable from one equation in the system of equations. Obviously, for even a moderately-sized system, many elimination matrices will be needed. However, we will see later that the elimination matrices can be easily inverted and combined into a single elimination matrix \(L\) that performs all elimination steps in a single matrix multiplication.
To start, consider the following \(3 \times 3\) system of equations where we want to solve for \(\vec{x},\) shown in both equation and \(A\vec{x} = \vec{b}\) form. \begin{align} \label{eq:elim_ex} \begin{matrix} 2 x_1 + 4 x_2 - 2 x_3 = 2\\ 4 x_1 + 9 x_2 - 3 x_3 = 8 \\ -2 x_1 -3 x_2 + 7 x_3 = 10 \end{matrix} &\qquad \qquad \equiv \qquad \qquad \begin{bmatrix} 2 & 4 & -2 \\ 4 & 9 & -3 \\ -2 & -3 & 7 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 2 \\ 8 \\ 10 \end{bmatrix}\\ \end{align}
If we were performing Gaussian elimination, the pivot \(p=2,\) the coefficient \(c=4,\) and the multiplier \(m=\frac{c}{p}=2.\) We would then perform \(eq_2^{\prime} = eq_2 - 2\,eq_1\) to remove \(x_1\) from \(eq_2.\)
Instead, we'll perform this using an elimination matrix \(E_{21},\) so subscripted because we're eliminating (adjusting to 0) coefficient \(a_{21}\) from \(A\) (i.e., we're eliminationg \(x_1\) from \(eq_2\).) First, we combined \(A\) and \(\vec{b}\) into a single matrix \(AB.\) \begin{equation} AB = \left[ \begin{array}{c c c | c} 2 & 4 & -2 & 2\\ 4 & 9 & -3 & 8\\ -2 & -3 & 7 & 10 \end{array} \right] \end{equation}
Next we take the multiplier \(m=2,\) negate it to represent subtraction, and place it in position \(e_{21}\) of a \(3 \times 3\) identity matrix \(E_{21}\). \begin{align} \label{eq:e_21} E_{21} &= \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}
Since the only difference between \(E_{21}\) and \(I_3\) lies in position \(e_{21},\) if we compute \(E_{21}\,AB,\) the only entries of AB that could possibly be changed are \(AB_{21},\) \(AB_{22},\) \(AB_{23},\) and \(AB_{24}.\) This corresponds to our goal: adjusting \(AB_{21}\) to 0 and updating the remaining values on row 2 of \(AB,\) exactly as if we'd performed \(eq_2 - 2\,eq_1.\) \begin{equation} AB^{\prime} = E_{21}\,AB = \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \left[ \begin{array}{c c c | c} 2 & 4 & -2 & 2 \\ 4 & 9 & -3 & 8 \\ -2 & -3 & 7 & 10 \end{array} \right] = \begin{bmatrix} 2 & 4 & -2 & 2 \\ 0 & 1 & 1 & 4 \\ -2 & -3 & 7 & 10 \end{bmatrix} \end{equation}
Notice that the coefficient for \(x_1\) in \(eq_2\) has adjusted to 0, exactly as we wanted. We could then eliminate the \(x_1\) coefficient in \(eq_3\) by computing the multiplier \(m=-1,\) negating it, and placing it in \(I_3\) at position \(i_{31}\) to create \(E_{31} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}.\) We could now eliminate \(x_1\) from both \(eq_1\) and \(eq_2\) by calculating \(E_{31}\,E_{21}\,AB.\) \begin{equation} AB^{\prime\prime} = E_{31}\,E_{21}\,AB = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 2 & 4 & -2 & 2 \\ 0 & 1 & 1 & 4 \\ -2 & -3 & 7 & 10 \end{bmatrix} = \begin{bmatrix} 2 & 4 & -2 & 2 \\ 0 & 1 & 1 & 4 \\ 0 & 1 & 5 & 12 \end{bmatrix} \end{equation}
Now we have our \(2 \times 2\) submatrix with two equations and two unknowns in the lower-right corner of the resulting matrix. To complete the example, we would zero \(ab_{32}^{\prime\prime}\) by calculating a multiplier of \(m=1,\) negating it, and inserting it into position \(e_{32}.\) \begin{equation} AB^{\prime\prime\prime} = E_{32}\,E_{31}\,E_{21}\,AB = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} 2 & 4 & -2 & 2 \\ 0 & 1 & 1 & 4 \\ 0 & 1 & 5 & 12 \end{bmatrix} = \begin{bmatrix} 2 & 4 & -2 & 2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 4 & 8 \end{bmatrix} \end{equation}
At this point we have \(4 x_3 = 8,\) or \(x_3 = 2.\) Back-substitution produces \(x_2 = 4 - x_3 = 4 - 2 = 2\) and \(\displaystyle x_1 = \frac{2 - 4 x_2 + 2 x_3}{2} = \frac{-2}{2} = -1,\) for a final solution of \(\vec{x} = \begin{bmatrix} -1 & 2 & 2 \end{bmatrix}^{T}.\) Substitution \(\vec{x}\) into Eqn \eqref{eq:elim_ex} confirms it is correct.
Permutation Matrix. To use elimination matrices for solving systems of equations, we need a matrix method for row exchange. This is known as a permutation matrix, and is a simple modification of the identity matrix. To exchange equations \(s\) and \(t,\) simply exchange the rows \(i_{s \ast}\) and \(i_{t \ast} \in I.\) For example, to exchange rows \(s=2\) and \(t=3\) in our previous example, we would use the permutation matrix \(p_{23}.\)
\begin{equation*} p_{23} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \end{equation*}This is simply \(I_3\) with rows \(2\) and \(3\) exchanged.
As far as I know, neither Python nor R has built-in code to perform Gaussian triangulation of a system of equations using elimination matrices. This is probably because there are other ways of solving \(A \vec{x} = \vec{b}\) (e.g., by using \(A^{-1}\)) that are directly available. It's not that difficult to write a small amount of code to perform Gaussian triangulation with elimination matrices, however. So, if you're curious, the code below should be able to do this in either Python or R. It takes the matrix of coefficients \(A\) for the system of equations and the values of \(\vec{b},\) then returns the upper-diagonal matrix \(A^{\prime}\,|\,\vec{b},\) or tells you the systems of equations cannot be diagonalized.
To complete our discussion of elimination matrices, we note how to directly compute their inverse. Consider elimination matrix \(E_{21}\) (Eqn \eqref{eq:e_21}) above. The \(-2\) in position \(e_{21}\) subtracts \(2 \, eq_1\) from \(eq_2.\) To reverse (or invert) this effect, we would add back \(2 \, eq_1\) to \(eq_2.\) This is easily done by replacing \(-2\) with \(2\) in \(E_{21}.\)
\begin{equation*} E_{21}^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{equation*}Any elimination matrix can be inverted by negating its off-diagonal value. If we calculated \(E_{21}^{-1} E_{21}\) we obtain \(I_3,\) exactly as required.
You may have wondered why we started our discussion of linear algebra by describing linear combinations (Eqn \eqref{eq:lin-comb}). Apart from an appropriate starting point, linear combinations are the requirement for a combination of column vectors forming a vector space. You already know a number of common vector spaces. For example, \(\mathbb{R}^2\) and \(\mathbb{R}^3,\) the collection of real numbers in 2D and 3D, are both vector spaces. So is \(\mathbb{Z},\) the vector space containing only the zero vector \(\textbf{0}.\) This is all fine, but what exactly defines a vector space?
Theoretically, given a vector space \(\mathbb{V}^{n},\) consider the linear combination \(\vec{w}\) of \(n\) vectors \(U = ( \vec{u_1}, \ldots, \vec{u_n} )\) = \(( \, [ u_{11}, u_{12}, \ldots, u_{1n} ]^{T}, \ldots, [ u_{n1}, u_{n2}, \ldots, u_{nn} ]^{T} \,), \; \vec{u_i} \in \mathbb{V}^{n}.\) The linear combination \(\vec{w} = c_1 \vec{u_1} + \cdots + c_n \vec{u_n}\) must also lie inside the same vector space, \(\vec{w} \in \mathbb{V}^{n}.\)
Gilbert Strang goes on to expand this into eight basic "requirements" a vector space must satisfy.
If the vectors in \(U\) are linearly independent and span \(\mathbb{V}^{n},\) then \(U\) forms a basis of \(\mathbb{V}^{n}.\)
You have already seen basis vectors before. For example, the basis vectors for \(\mathbb{R}^2\) are normally the \(x\) and \(y\) axes \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) and \(\begin{bmatrix} 0 \\ 1 \end{bmatrix}.\) These axes are orthogonal to one another, so they are linearly independent. And, any point \(p = \begin{bmatrix} p_1 \\ p_2 \end{bmatrix} \in \mathbb{R}^2\) can be formed by the linear combination \(p_1 \begin{bmatrix} 1 \\ 0 \end{bmatrix} + p_2 \begin{bmatrix} 0 \\ 1 \end{bmatrix}.\)
Subspaces are subsets of a vector space that satisfy three specific requirements. For example, in \(\mathbb{R}^3\) any 2D plane is a subspace of \(\mathbb{R}^3.\) So is any line with 3D endpoints, or any 3D point. Not surprisingly, a subspace has a specific theoretical definition. Given \(\vec{u}\) and \(\vec{v}\) in a subspace \(S_S,\) then for any scalar \(c\):
We often say the set of vectors in \(S_S\) contains the zero vector and is "closed" under addition and multiplication, or in other words, linear combinations of vectors in \(S_S\) stay in \(S_S.\) This means a subspace is itself a vector space.
Remember that our ultimate goal is to solve \(A\vec{x} = \vec{b}.\) If \(A\) is NOT invertable, then \(A\vec{x} = \vec{b}\) is solvable for some \(\vec{b},\) but not for others. If we choose a concrete \(\vec{x},\) say \(\vec{x_i},\) \(A \vec{x_i} = \vec{b_i}.\) If we take all possible \(\vec{x_i}\) we generate a collection of all possible \(\vec{b_i}\) called \(B.\) Now, for any \(\vec{b_j},\) if \(\vec{b_j} \in B,\) then \(\exists \, \vec{x_j}\) giving \(A \vec{x_j} = \vec{b_j}.\) If \(\vec{b_j} \notin B,\) then no such \(\vec{x_j}\) exists. We say that \(B\) forms the column space of \(A,\) the set of all possible \(\vec{b_i}\) that can be formed by \(A \vec{x}.\)
The simplest way to generate \(B\) is to divide \(A\) into its individual columns, then generate all possible linear combinations of those columns. Note that this is equivalent to generating all possible \(\vec{x},\) since if we view \(A \vec{x}\) as a combination of columns (Eqn \eqref{eq:vec_mult}), we have exactly this linear combination. \begin{equation} A\vec{x} = x_1 A_{\ast 1} + \cdots + x_n A_{\ast n} \end{equation}
Consider a practical example, \(A = \begin{bmatrix}1 & 0\\4 & 3\\2 & 3\end{bmatrix} \begin{bmatrix}x_1 \\ x_2\end{bmatrix}.\) Since \(A\) is not square, it has no inverse. This is the equation of a plane in \(\mathbb{R}^3,\) so all solutions \(\vec{b_i}\) lie in the column space \(C(A),\) or in other words, on the plane formed by \(A \vec{x}.\)
The nullspace \(N(A)\) is the set of all solutions to \(A\vec{x}=\textbf{0}.\) That is, we replace the general \(\vec{b}\) with the zero vector, \(\vec{b} = \textbf{0}.\) We do this to describe methods to solve \(A\vec{x} = \textbf{0}\) that will later be very helpful in solving the full equation \(A\vec{x} = \vec{b}.\)
Just like column space \(C(A),\) the nullspace \(N(A)\) is a subspace, specifically, a subspace of \(\mathbb{R}^n.\) As a practical example, consider \(A = \begin{bmatrix} 1 & 2\\3 & 6\end{bmatrix}.\) We apply Gaussian elimination to determine values for \(x_1\) and \(x_2.\)
\begin{equation*} \begin{aligned} x_1 + 2 x_2 &= 0\\ 3 x_1 + 6 x_2 &= 0\\ \end{aligned} \qquad \Longrightarrow \qquad \begin{aligned} x_1 +2 x_2 &= 0\\ 0 &= 0\\ \end{aligned} \end{equation*}The second equation \(0 = 0\) tell us \(A\) is singular. We can see this by recognizing the second row \(A_{2 \ast}\) is three times the first row of \(A, A_{2 \ast} = 3 \, A_{1 \ast}.\) Since this gives us one equation and two unknowns, there is no single solution \((x_1,x_2)\) to \(A \vec{x} = \textbf{0}.\) The equation \(x_1 + 2 x_2 = 0 \equiv x_2 = -\frac{1}{2}x_1\) is a line passing through the origin (note that every nullspace MUST include the origin, since the zero vector \(\textbf{0}\) is always a solution to \(A \vec{x} = \textbf{0}\)). Any point on this line is a solution to \(A \vec{x} = \textbf{0}.\) To describe these solutions in an efficient way, we take the free component \(x_2\) and set it to a constant value or "special solution" \(x_2 = 1.\) This defines \(x_1 = -2 x_2 = -2.\) Now, \(N(A) = c \begin{bmatrix} -2 & 1 \end{bmatrix}^{T}\) for any scalar \(c.\)
If there are no free components then the only solution to \(A \vec{x} = \textrm{0}\) is the zero vector \(\vec{0}\) and the nullspace is the zero vector only, \(N(A) = \mathbb{Z}.\) An obvious situation where this occurs is when \(A\) is square and invertable. Otherwise, we need to identify the free component(s), and assign special solution values (usually 0 and 1) to determine all possible solutions to our equation. As a practical example, consider \(Ax = \begin{bmatrix} 1 & 2 & 2 & 4 \\ 3 & 8 & 6 & 16 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x3 \\ x4 \end{bmatrix} = 0 \equiv \; \begin{matrix} x_1 + 2 x_2 + 2 x_3 + 4 x_4 \\ 3 x_1 + 8 x_2 + 6 x_3 + 16 x_4 \end{matrix} = 0.\) Here, we have two (non-trivial) equations and four variables, so we intuitively anticipate having free components. If we use Gaussian elimination to eliminate \(x_1\) from the second row, \(A_{2 \ast}^{\prime} = A_{2 \ast} - 3 A_{1 \ast},\) we obtain an upper-triangular matrix \(U.\) \begin{equation} U = \begin{bmatrix} \textbf{1} & 2 & 2 & 4 \\ 0 & \textbf{2} & 0 & 4 \end{bmatrix} \end{equation}
We could extend \(U\) to row echelon form by recognizing that if we added two additional rows \(A_{3 \ast} = \begin{bmatrix} 0 & 0 & 0 & 0 \end{bmatrix} \) and \(A_{4 \ast} = \begin{bmatrix} 0 & 0 & 0 & 0 \end{bmatrix} \). This simply produces two additional equations \(0 x_1 + 0 x_2 + 0 x_3 + 0 x_4 = 0\) which is equivalent to allowing any values of \((x_1, x_2, x_3, x_4)\). This also extends \(U\) to row echelon form \(U = \begin{bmatrix} 1 & 2 & 2 & 4 \\ 0 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\).
To solve for \((x_1, x_2, x_3, x_4)\) we use an approach very similar to Gaussian elimination. First, assume there are \(p\) pivots. This means there are \(n-p\) "free" components. In our example, \(p=2\) and \(n=4\) so there are \(4-2=2\) free components \(x_3\) and \(x_4\). We can choose any values we want for the free components. Normally, we we use a simple approach to define free component values. Each free component is given an opportunity to equal \(1\) while all other free components equal \(0\). Given \(n-p\) free components, we need an additional \(n-p\) equations to solve \(Ax=b\), and each additional equation needs unique free component values (otherwise the equations would not be independent and would not correspond to unique equations.) Applying our simple approach for free variable assigniment yields \(s_1 = (x_3=1,x_4=0)\) and \(s_2=(x_3=0,x_4=1)\). If we solve for \(x_1\) and \(x_2\) using the values defined by \(s_1\) we obtain \(\begin{bmatrix} -2 & 0 & 1 & 0 \end{bmatrix}^{T}.\) Similarly, using the values defined by \(s_2\) produces \(\begin{bmatrix} 0 & -2 & 0 & 1 \end{bmatrix}^{T}\). As an aside, because \(s_1 \cdot s_2 = 0\) and \(s_1\) and \(s_2\) are orthogonal they define a plane in 3D space, since one way to define a 3D plane is by specifying two orthogonal 2D lines. This means all solutions to \(A \vec{x} = \textrm{0}\) lie on this plane: \(N(A)= c_1 \begin{bmatrix} -2 & 0 & 1 & 0 \end{bmatrix}^{T} + c_2 \begin{bmatrix} 0 & -2 & 0 & 1 \end{bmatrix}^{T}\) for scalar values \(c_1\) and \(c_2.\)
Reduced Row Echelon Form. As a further simplifying step, we often continue to manipulate \(U\) to have the following two properties.
This provides two useful properties. First, it makes it very easy to determine the values for the special vectors \(s_i.\) Second, it allows us to immediately determine the rank of \(A.\) Consider \(U\) from our last example. We will convert it to a reduced row echelon matrix \(R.\) \begin{equation} \begin{array}{c c c} U = \begin{bmatrix} 1 & 2 & 2 & 4 \\ 0 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} & \quad \Longrightarrow \quad & R = \begin{bmatrix} \textrm{1} & \textrm{0} & 2 & 0 \\ \textrm{0} & \textrm{1} & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{array} \end{equation}
Simple Gaussian-like elimination was used to generate \(R.\) To produce a 0 in position \(u_{12}\) the second row of \(U\) was subtracted from the first, \(R_{1 \ast} = U_{1 \ast} - U_{2 \ast}.\) To produce a 1 at pivot position \(u_{22}\) the second row of \(U\) was divided by 2, \(R_{2 \ast} = \frac{1}{2} U_{2 \ast}.\)
How is \(R\) useful? First, each non-pivot column represents a free variable. Since the third and fourth columns are non-pivot columns, they represent free solutions: \(x_1 = -2 x_3\) and \(x_2 = -2 x_4\). If we chose the same two free solution pairs as before, \((x_3=1,x_4=0)\) and \((x_3=0,x_4=1)\) we would obtain the same solutions: \([-2, 0, 1, 0]^{T}\) and \([0, -2, 0, 1]^{T}\). This simply shows that the reduced row echelon form is identical and produces identical solutions to the row echelon form.
If this is true, why do we care about reduced row echelon form? There are a number of situations where it can be helpful. One that is most relevant here is to solve for the nullspace of \(A\) directly. It is described as a "trick" by Strang. If we use our strategy of choosing free variable values as \((1,0,\ldots,0), \ldots, (0,0,\ldots,1)\), then we can take the free variable values in the non-pivot columns and reverse their sign. These then represent the pivot variable values for the corresponding free variable vector.
For example, our non-pivot columns are \([2, 0, 0, 0]^{T}\) and \([0, 2, 0, 0]^{T}\). For the first pair of free variables \((x_3=1,x_4=0)\) we take the first non-pivot column, reverse the sign of its values giving \([-2, 0, 0, 0]^{T}\) and insert \(x_3\) and \(x_4\), producing the solution \([-2, 0, 1, 0]^{T}.\). This is exactly the first solution we calculated above. Similarly, using the second pair of free variables \((x_3,x_4=1)\) gives solution \([0, -2, 0, 1]^{T}\). So the reduced row echelon form coupled with our strategy of free variable selection provides a way to solve for \(x_1\) and \(x_2\) directly, without having to solve an equation.
Both Python and R have built-in functions to return reduced row echelon matrices.
The second important property of \(R\) is it defines the rank of \(A.\) \(A\) is a \(2 \times 4\) matrix, but this is not the true size of the linear system it defines. If there were two identical rows in \(A,\) the second would disappear during elimination. If one row is a linear combination of another, that row would also disappear during elimination. When we talk about the true size of a matrix, we are talking about its rank. The rank \(r\) of a matrix is the number of (non-zero) pivots contained in the matrix.
The reduced echelon form of \(A\) eliminates all dependent rows, giving us an exact pivot count and corresponding rank \(r.\) The rank of \(A = \begin{bmatrix} 1 & 2 & 2 & 4 \\ 3 & 8 & 6 & 16 \end{bmatrix}\) in our previous example is \(r=2.\)
The final reduced echelon matrix \(R\) contains \(r\) non-zero rows. Consider a new \(A = \begin{bmatrix} 1 & 1 & 2 & 4 \\ 1 & 2 & 2 & 5 \\ 1 & 3 & 2 & 6 \end{bmatrix}.\) The reduced echelon form of \(A\) is \(R = \begin{bmatrix} 1 & 0 & 2 & 3 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}.\) Here, \(r=2\) and \(R\) has two non-zero rows. Intuitively, we can see that the first two columns of \(A\) are \(R_{\ast 1} = (1,1,1)\) and \(R_{\ast 2} = (1,2,3),\) which point in different directions. These form the pivot columns in \(R.\) The third column \(R_{\ast 3} = (2,2,2)\) is a multiple of the first, so it will be eliminated. The fourth column \(R_{\ast 4} = (4,5,6)\) is the sum of the first three columns, so it will also be eliminated. Since there are two independent columns in \(A,\) it produces two pivots and a rank of \(r=2.\)
One final use of rank is to determine whether a square matrix \(A\) of size \(n \times n\) contains a unique solution. If rank \(r = n\) then \(A\) is said to be full rank and there is only one solution to \(A\vec{x} = \vec{b},\) if a solution exists. When \(r = n\) all of the columns are independent of one another, so we have \(n\) equations and \(n\) unknowns, exactly what we need to find a single solution to \(A \vec{x} = \vec{b}.\)
At this point, we finally have what we need to fully solve \(A\vec{x} = \vec{b}\) for any \(\vec{b}\) and not only \(\vec{b} = \textrm{0},\) which provided solution(s) to the nullspace \(N(A).\) Since \(\vec{b}\) is no longer \(\textrm{0},\) it must be considered when we manipulate \(A.\) As we did previously, we will augment \(A\) by appending \(\vec{b}\) as a new column, producing \(\begin{bmatrix} A & \vec{b} \end{bmatrix}.\) When we apply elimination operations to generate \(R,\) we will also be applying them to \(\vec{b}.\) Consider the following practical example, with the original \(A \vec{x} = \vec{b}\) on the left, and the augmented matrix \(\begin{bmatrix} A & \vec{b} \end{bmatrix}\) on the right. \begin{equation} \begin{array}{c c c} \begin{bmatrix} 1 & 3 & 0 & 2 \\ 0 & 0 & 1 & 4 \\ 1 & 3 & 1 & 6 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 1 \\ 6 \\ 7 \end{bmatrix} & \quad \Longrightarrow \quad & \begin{bmatrix} 1 & 3 & 0 & 2 & \textrm{1} \\ 0 & 0 & 1 & 4 & \textrm{6} \\ 1 & 3 & 1 & 6 & \textrm{7} \end{bmatrix} = \begin{bmatrix} A & \vec{b} \end{bmatrix} \end{array} \end{equation}
If we subtract row 1 from row 3, then subtract row 2 from row 3, we produce \(R\) with pivot columns 1 and 3 and free columns 2 and 4. Column 5, which originally contained \(\vec{b},\) has changed to \(\vec{d} = \begin{bmatrix} 1 & 6 & 0 \end{bmatrix}^{T}.\) \begin{equation} \label{eq:full_soln} \begin{bmatrix} 1 & 3 & 0 & 2 & \textrm{1} \\ 0 & 0 & 1 & 4 & \textrm{6} \\ 0 & 0 & 0 & 0 & \textrm{0} \end{bmatrix} = \begin{bmatrix} R & \vec{d} \end{bmatrix} \end{equation}
Examining \(\begin{bmatrix} R & \vec{d} \end{bmatrix}\) shows rank \(r=2\) and two free variables \(x_2\) and \(x_4\) corresponding to columns without pivots. To find one particular solution \(x_p\) to the equation \(A \vec{x} = \vec{b},\) one method guaranteed to work is to set the free variables \(x_2\) and \(x_4\) to 0, then solve for the pivot variables \(x_1\) and \(x_3.\) This produces \(\vec{x} = \begin{bmatrix} 1 & 0 & 6 & 0 \end{bmatrix}^{T}.\) To simplify further, since the pivot columns form the identity matrix, we can simply set the free variables to 0 and the pivot variables to their corresponding values in \(\vec{d} = \begin{bmatrix} \textrm{1} & 0 & \textrm{6} & 0 \end{bmatrix}.\)
Remember that \(R\) also allows us to determine the special solutions to the nullspace \(N(A).\) Based on \(R\) in Eqn \eqref{eq:full_soln}, and choosing free variable values \((x_2=1,x_4=0)\) and \((x_2=0,x_4=1)\), we have \(c_1 R_{\ast 1} + c_2 R_{\ast 2} + c_3 R_{\ast 3} = \mathbf{\vec{0}}\)\(\; \Rightarrow \;\) \(R_{\ast 2} = -3\,R_{\ast 1} + 0\,R_{\ast 3}\) and \(c_1 R_{\ast 1} + c_3 R_{\ast 3} + c_4 R_{\ast 4} = \mathbf{\vec{0}}\)\(\; \Rightarrow \;\)\(R_{\ast 4} = -2\,R_{\ast 1} - 4\,R_{\ast 3}.\) This produces two special solutions \(x_n = (x_2 \begin{bmatrix} -3 & 1 & 0 & 0 \end{bmatrix}^{T}, x_4 \begin{bmatrix} -2 & 0 & -4 & 1 \end{bmatrix}^{T}).\) The full set of all possible solutions to \(A \vec{x} = \vec{b}\) is defined as \(x = x_p + x_n = \begin{bmatrix} 1 \\ 0 \\ 6 \\ 0 \end{bmatrix} + x_2 \begin{bmatrix} -3 \\ 1 \\ 0 \\ 0 \end{bmatrix} + x_4 \begin{bmatrix} -2 \\ 0 \\ -4 \\ 1 \end{bmatrix}.\)
You might wonder, why are there more than one solution to \(A \vec{x} = \vec{b}\)? This is because \(A\) is not a square, invertable matrix. If that were the case, then the nullspace \(N(A)\) would only contain the \(\vec{0}\) vector, and there would be a single solution \(x_p\) since \(x_n = \emptyset.\) This is a special case of the example shown here, but it is the one that most often occurs.
Factorization is the process of converting a matrix \(A\) into multiple "special" matrices that, when multiplied, return \(A.\) We will demonstrate this approach using the elimination matrices discussed in the previous section. The goal of elimination is to convert \(A\) into an upper-triangular matrix \(U\) through a series of individual elimination steps \(E = \prod E_{ij}.\) If we take the equation \(EA = U\) and generate a lower-triangular matrix \(L = E^{-1},\) then \((LE)A = LU \Rightarrow A = LU.\) In other words, we have factorized \(A\) into the inverse of the product of the elimination matrices \(E^{-1}=L\) and the target upper-triangular matrix \(U.\)
We already saw how to compute \(U\) in the Elimination section. Let's again start by assuming no row exchanges are needed, which means no permutation matrices are generated. How do we calculate \(L\)? Since this is a combination of elimination matrices, and elimination matrices are slight variations on identify matrices, this turns out to be very simple. Consider a simple \(A\) of shape \(2 \times 2.\) Here, we only need one elimination matrix \(E_{21}\) to eliminate \(x_1\) in \(eq_2.\) If we wanted to take \(U\) and convert it back to \(A,\) we would use the inverse operation \(E_{21}^{-1}.\) \begin{align} \label{eq:LU_A} \begin{split} \textrm{Forward from} \; A \; \textrm{to} \; U: \quad E_{21}A &= \begin{bmatrix} 1 & 0 \\ -3 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 6 & 8 \end{bmatrix} &= \begin{bmatrix} 2 & 1 \\ 0 & 5 \end{bmatrix} &= U\\ \textrm{Backward from} \; U \; \textrm{to} \; A: \quad E_{21}^{-1}U &= \begin{bmatrix} 1 & 0 \\ 3 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 5 \end{bmatrix} &= \begin{bmatrix} 2 & 1 \\ 6 & 8 \end{bmatrix} &= A\\ \end{split} \end{align}
The second line of Eqn \eqref{eq:LU_A} is the factorization \(LU = A.\) Here, \(L = E_{21}^{-1},\) since there is only one elimination matrix used to convert \(A\) to \(U.\) If \(A\) were a larger matrix, then \(L\) would include the reverse product of all the inverse elimination matrices. For example, if \((E_{32} E_{31} E_{21})A = U,\) then \(A = (E_{21}^{-1} E_{31}^{-1} E_{32}^{-1}) U,\) or \(L = E_{21}^{-1} E_{31}^{-1} E_{32}^{-1}.\)
Because \(E_{ij}^{-1}\) is so similar to \(I\) and because it is always a lower-triangular matrix (the non-zero off-diagonal entry is below the diagonal), there is a very simple and convenient way to convert the product of the inverse elimination matrices into a single matrix \(L\) without complicated matrix multiplication.
Practical Example. Consider \(A = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{bmatrix}.\) The three elimination matrices \(E_{21},\) \(E_{31},\) and \(E_{32}\) are used to convert \(A\) to upper-triangular matrix \(U.\) \begin{align} \begin{split} E_{21} &= \begin{bmatrix} 1 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \quad E_{31} &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \quad E_{32} &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{2}{3} & 1 \end{bmatrix} \quad (E_{32}\,E_{31}\,E_{21})A = U &= \begin{bmatrix} 2 & 1 & 0 \\ 0 & \frac{3}{2} & 1 \\ 0 & 0 & \frac{4}{3} \end{bmatrix} \end{split} \end{align}
We can use the steps enumerated above to directly compute \(L\) from the three elimination matrices. \begin{align} L &= \begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & 1 & 0 \\ 0 & \frac{2}{3} & 1 \end{bmatrix} \end{align}
And, indeed, \(LU = A\) as expected. \begin{align} LU &= \begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & 1 & 0 \\ 0 & \frac{2}{3} & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 & 0 \\ 0 & \frac{3}{2} & 1 \\ 0 & 0 & \frac{4}{3} \end{bmatrix} = \begin{bmatrix} 2 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{bmatrix} = A \end{align}
Balance. \(LU\) is sometimes called unbalanced or "non-symmetric" because the diagonal entries on \(U\) are not 1s. Common terminology for the diagonal entries on \(U\) are the pivots of \(U.\) This corresponds to our previous notion of pivot: the first non-zero coefficient of an equation (a row in \(U\)) in a system of equations. Since \(U\) is an upper-triangular matrix, the entries on the diagonals are the first non-zero entry on each row. This is why they are often called pivots.
If we want to correct for balance, we can factorize \(U\) into two matrices \(D\)\(U^{\prime}\) = \(U\) by taking the pivots \(p_1, p_2, \ldots, p_n\) on the diagonal of \(U,\) placing them on the diagonal of \(D = \mathbf{0},\) then dividing each row in \(U\) by its corresponding pivot. \begin{equation} DU^{\prime} = \begin{bmatrix} p_1 & 0 & \cdots & 0 \\ 0 & p_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & p_n \end{bmatrix} \begin{bmatrix} 1 & \frac{u_{12}}{p_1} & \frac{u_{13}}{p_1} & \cdots & \frac{u_{1n}}{p_1} \\ 0 & 1 & \frac{u_{23}}{p_2} & \cdots & \frac{u_{2n}}{p_2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{bmatrix} = U \end{equation}
Now, we rewrite \(A = LDU^{\prime}\) (or often simply \(A=LDU\) with the assumption that the original \(U\) is replaced with \(U^{\prime}.\)) It is assumed that \(U\) has 1s on its diagonal. As a practical example, consider the following \(2 \times 2\) matrices. \begin{equation*} \begin{array}{c c c} LU & & LDU^{\prime}\\ \begin{bmatrix} 1 & 0 \\ 3 & 1 \end{bmatrix} \begin{bmatrix} 2 & 8 \\ 0 & 5 \end{bmatrix} &\qquad \Longrightarrow \qquad & \begin{bmatrix} 1 & 0 \\ 3 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & 5 \\ \end{bmatrix} \begin{bmatrix} 1 & 4 \\ 0 & 1 \\ \end{bmatrix} \end{array} \end{equation*}
The only remaining issue in using factorization to perform elimination is row exchange. We saw above how row exchange can be performed with a permutation matrix \(P,\) where \(P\) begins as an identity matrix and rows of \(P\) are swapped to perform equation swapping. Although there are a variety of ways to integrate the permutation matrix into our \(A = LU = LDU\) factorization, the preferred method is to place \(P\) to the left of \(A.\) This performs row swapping first, guaranteeing no pivots of \(p=0\) during the elimination process. \begin{equation} PA = LU = LDU^{\prime} \end{equation}
With this final formula, solving systems of linear equations through elimination is presented as a factorization of \(PA\) into a lower-triangular matrix \(L\), a diagonal matrix \(D\), and an upper-triangular matrix \(U\).
Both Python and R have built-in LU factorization functions.
A second common factorization technique is QR factorization. Given an \(m \times n\) matrix \(A\) with linearly independent columns, QR factorization decomposes \(A=QR\) into an \(m \times n\) matrix \(Q\) with orthonormal columns (\(Q_{\ast i} \cdot Q_{\ast j}) = 0,\) \(||Q_{\ast i}|| = ||Q_{\ast j}|| = 1,\) and an upper-triangular \(n \times n\) matrix \(R.\) \begin{equation} \label{eq:QR} A = \begin{bmatrix} A_{\ast 1} & A_{\ast 2} & \cdots & A_{\ast n} \end{bmatrix} = \begin{bmatrix} Q_{\ast 1} & Q_{\ast 2} & \cdots & Q_{\ast n} \end{bmatrix} \begin{bmatrix} A_{\ast 1} \cdot Q_{\ast 1} & A_{\ast 2} \cdot Q_{\ast 1} & \cdots & A_{\ast n} \cdot Q_{\ast 1}\\ 0 & A_{\ast 2} \cdot Q_{\ast 2} & \cdots & A_{\ast n} \cdot Q_{\ast 2}\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & A_{\ast n} \cdot Q_{\ast n} \end{bmatrix} = QR \end{equation}
Technically, QR factorization is an efficient matrix-based method for performing the Gram-Schmidt process. Gram-Schmidt converts a basis into an orthonormal basis with orthogonal, unit-length basis axes. Clearly, if we are talking about the real vector space \(\mathbb{R}^{n},\) then the vectors \(\begin{bmatrix}1 & 0 & \cdots & 0\end{bmatrix}^{T},\) \(\begin{bmatrix}0 & 1 & \cdots & 0\end{bmatrix}^{T},\) \(\ldots,\) \(\begin{bmatrix}0 & 0 & \cdots & 1\end{bmatrix}^{T}\) are the obvious choice. However, when the vector space is more complicated, it may not be as straight-forward to convert an arbitrary set of basis vectors into a much more useful set of orthonormal basis vectors. We will also see that QR factorization can be used to solve other important problems. In fact, we use QR factorization to solve the linear least squares problem later in these notes.
Values for \(Q\) are solved using Gram-Schmidt. Once \(Q\) is defined, its values are dotted with corresponding entries in \(A\) to calculate entries in \(R\) (Eqn \eqref{eq:QR}). \begin{alignat}{2} \begin{split} \vec{u_1} &= A_{\ast 1} & \qquad Q_{\ast 1} &= \frac{\vec{u_1}}{||\vec{u_1}||}\\ \vec{u_2} &= A_{\ast 2} - ( A_{\ast 2} \cdot Q_{\ast 1} ) Q_{\ast 1} & \qquad Q_{\ast 2} &= \frac{\vec{u_2}}{||\vec{u_2}||}\\ \vec{u_{k+1}} &= A_{\ast (k+1)} - (A_{\ast (k+1)} \cdot Q_{\ast 1}) Q_{\ast 1} - \cdots - (A_{\ast (k+1)} \cdot Q_{\ast k}) Q_{\ast k} & \qquad Q_{\ast (k+1)} &= \frac{\vec{u_{k+1}}}{||u_{\vec{k+1}}||} \end{split} \end{alignat}
Practical Example. Given \(A = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix},\) its QR factorization is constructed as follows. \begin{align} \begin{split} \vec{u_1} &= A_{\ast 1} = \begin{bmatrix} 1 & 1 & 0 \end{bmatrix}^{T}\\ Q_{\ast 1} &= \frac{\vec{u_1}}{||\vec{u_1}||} = \frac{1}{\sqrt{2}} \vec{u_1} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \end{bmatrix}^{T}\\[8pt] \vec{u_2} &= A_{\ast 2} - ( A_{\ast 2} \cdot Q_{\ast 1} ) Q_{\ast 1}\\ &= \begin{bmatrix} 1 & 0 & 1 \end{bmatrix}^{T} - \frac{1}{\sqrt{2}} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \end{bmatrix}^{T} = \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} & 1 \end{bmatrix}^{T}\\ Q_{\ast 2} &= \frac{\vec{u_2}}{||\vec{u_2}||} = \frac{1}{\sqrt{\frac{3}{2}}} \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} & 1 \end{bmatrix}^{T} = \begin{bmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} \end{bmatrix}^{T}\\[8pt] \vec{u_3} &= A_{\ast 3} - ( A_{\ast 3} \cdot Q_{\ast 1} ) Q_{\ast 1} - ( A_{\ast 3} \cdot Q_{\ast 2} ) Q_{\ast 2} \\ &= \begin{bmatrix} 0 & 1 & 1 \end{bmatrix}^{T} - \frac{1}{\sqrt{2}} \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \end{bmatrix}^{T} - \frac{1}{\sqrt{6}} \begin{bmatrix} \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} \end{bmatrix}^{T} = \begin{bmatrix} -\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{bmatrix}^{T}\\ Q_{\ast 3} &= \frac{\vec{u_3}}{||\vec{u_3}||} = \begin{bmatrix} -\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{bmatrix}^{T} \end{split} \end{align}
These results define \(Q.\) \begin{equation} Q = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}}\\ 0 & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}}\\ \end{bmatrix} \end{equation}
\(A\) and \(Q\) are then combined to define \(R.\) \begin{equation} R = \begin{bmatrix} \frac{2}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ 0 & \frac{3}{\sqrt{6}} & \frac{1}{\sqrt{6}}\\ 0 & 0 & \frac{2}{\sqrt{3}} \end{bmatrix} \end{equation}
The results can be checked to validate that \(QR\) factors \(A\) as expected. \begin{equation} A = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}}\\ 0 & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}}\\ \end{bmatrix} \begin{bmatrix} \frac{2}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ 0 & \frac{3}{\sqrt{6}} & \frac{1}{\sqrt{6}}\\ 0 & 0 & \frac{2}{\sqrt{3}} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix} = QR \end{equation}
Although we will not go through all the steps to derive \(Q\) and \(R,\) here is an example where \(A\) is "tall", \(m > n.\) \begin{align} \begin{split} A = \begin{bmatrix} -1 & -1 & 1 \\ 1 & 3 & 3 \\ -1 & -1 & 5 \\ 1 & 3 & 7 \end{bmatrix} &= \begin{bmatrix} \vec{q_1} & \vec{q_2} & \vec{q_3} \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ 0 & r_{22} & r_{23} \\ 0 & 0 & r_{33} \\ \end{bmatrix} \\ &= \begin{bmatrix} -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix} \begin{bmatrix} 2 & 4 & 2 \\ 0 & 2 & 8 \\ 0 & 0 & 4 \end{bmatrix}\\ &= QR\\ \end{split} \end{align}
Both Python and R have built-in QR factorization functions.
An interesting property of any \(A\) with linearly independent columns is a pseudo-inverse \(A^{\dagger}\) of \(A\) exists, even if \(A\) is "tall" and not square. \begin{equation} A^{\dagger} = (A^{T}A)^{-1} A^{T} \end{equation}
The pseudo-inverse is sometimes called the Moore-Penrose inverse, after the mathematicians Eliakim Moore and Roger Penrose who proposed it. If \(A\) is square, \(A^{\dagger}\) reduces to the normal inverse \(A^{-1}.\) \begin{equation} A^{\dagger} = (A^{T} A)^{-1} A^{T} = A^{-1} A^{-T} A^{T} = A^{-1} I = A^{-1} \end{equation}
If \(A\) is "tall" and \(m > n,\) then \(A^{\dagger}\) is an \(n \times m\) matrix.
Practical Example. Consider \(A = \begin{bmatrix} -1 & -1 & 1 \\ 1 & 3 & 3 \\ -1 & -1 & 5 \\ 1 & 3 & 7 \end{bmatrix} .\) The pseudoinverse \(A^{\dagger}\) is calculated as follows. \begin{align} \begin{split} A^{\dagger} &= (A^{T} A)^{-1} A^{T}\\ &= \left( \begin{bmatrix} -1 & 1 & -1 & 1\\ -1 & 3 & -1 & 3\\ 1 & 3 & 5 & 7 \end{bmatrix} \begin{bmatrix} -1 & -1 & 1 \\ 1 & 3 & 3 \\ -1 & -1 & 5 \\ 1 & 3 & 7 \end{bmatrix} \right)^{-1} \begin{bmatrix} -1 & 1 & -1 & 1\\ -1 & 3 & -1 & 3\\ 1 & 3 & 5 & 7 \end{bmatrix}\\ &= \begin{bmatrix} 4 & 8 & 4 \\ 8 & 20 & 24 \\ 4 & 24 & 84 \\ \end{bmatrix}^{-1} \begin{bmatrix} -1 & 1 & -1 & 1\\ -1 & 3 & -1 & 3\\ 1 & 3 & 5 & 7 \end{bmatrix}\\ A^{\dagger} &= \begin{bmatrix} -1.625 & -1.125 & 0.125 & 0.625\\ 0.75 & 0.75 & -0.25 & -0.25\\ -0.125 & -0.125 & 0.125 & 0.125 \end{bmatrix} \end{split} \end{align}
Both Python and R have built-in pseudo-inverse functions.
R also has a ginv() function to implement the generalized
inverse as part of its MASS library.
Like the pseudo-inverse, the generalized inverse (or g-inverse) of a matrix \(A\) is a matrix \(A^{g}\) that has some but not necessarily all properties of an inverse. A matrix \(A^{g} \in \mathbb{R}^{n \times m}\) is a generalized inverse of \(A \in \mathbb{R}^{m \times n}\) if \(A A^{g} A = A.\)
To motivate this concept, consider our standard system of linear equations \(A \vec{x} = \vec{b}\) with \(A \in \mathbb{R}^{m \times n}\) containing \(m\) rows and \(n\) columns. If \(A\) is nonsingular, then \(\vec{x} = A^{-1} \vec{b}\) is the unique solution to the equation.
If, however, \(A\) is rectangular or singular, then no \(A^{-1}\) exists. We need a candidate \(A^{g}\) with \(n\) rows and \(m\) columns that satisfies the following equation. \begin{equation} A A^{g} \vec{b} = \vec{b} \end{equation}
In other words, \(\vec{x} = A^{g} \vec{b}\) is a solution to the linear system of equations \(A \vec{x} = \vec{b}.\) This is another way of saying we need a matrix \(A^{g}\) of order \(m \times n\) s.t. \begin{equation} A A^{g} A = A \end{equation}
As with the pseudo-inverse, the generalized inverse is equal to the regular inverse \(A^{-1}\) when it exists.
A collection of Penrose conditions have been defined for generalized inverse matrices \(A^{g}.\)
Here, \(^{*}\) represents the conjugate transpose. Note. The complex conjugate of a real number with no imaginary part is just the number itself, \(\overline{x} = x\), so the complex conjugate of a real-valued matrix \(A\) is simply \(A^{T}\), since the complex conjugate of each \(a_{ij} \in A^{T}\) is \(a_{ij}.\)
If \(A\) satisfies condition 1, it is a generalized inverse. If it satisfies all four conditions, it is a pseudo-inverse.
Recall we have already discussed the determinant to a \(2 \times 2\) square matrix \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\) in Eqn \eqref{eq:det_2x2}. The determinant of \(A\) cross-multiplies and subtracts such that \(\textrm{det}(A) = |A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc.\) The reciprocal of determinant \(|A|\) acts as a scalar to a reordered version of \(A\) to calculate its inverse \(\displaystyle A^{-1} = \frac{1}{|A|} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}.\) If \(|A|=0\) then \(A\) is singular and cannot be inverted.
What if square matrix \(A\) has \(n > 2?\) To solve for \(|A|\) we must define minors and cofactors. Take any entry \(a_{ij} \in A\) and delete row \(i\) and column \(j.\) The determinant of the resulting \((n-1) \times (n-1)\) submatrix is called the minor \(M_{ij}\) of \(a_{ij}.\) As a practical example, consider a \(3 \times 3\) matrix with the center entry \(a_{22}\) removed. \begin{equation} \begin{array}{c c c} A = \begin{bmatrix} a_{11} & \columncolor{lightblue} a_{12} & a_{13} \\ \rowcolor{lightblue} a_{21} & \mathbf{a_{22}} & a_{32} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} & \quad \Longrightarrow \quad & M_{22} = \begin{vmatrix} a_{11} & a_{13} \\ a_{31} & a_{33} \end{vmatrix} \end{array} \end{equation}
The cofactor \(C_{ij}\) of \(a_{ij}\) is the minor \(M_{ij}\) with its sign set to positive or negative: positive if \(i + j\) is even, and negative if \(i + j\) is odd. \begin{equation} C_{ij} = (-1)^{i+j} M_{ij} \end{equation}
Cofactors are used to calculate the determinant of \(A.\) Take any row \(i\) of \(A.\) The determinant \(|A|\) is the sum of the entries along row \(i\) times their cofactors. \begin{equation} |A| = \sum_{j=1}^{n} a_{ij} C_{ij} \;\; \textrm{for any} \; 1 \leq i \leq n \end{equation}
The sum of a column's entries times its cofactors can also be used to calculate the determinant of \(A.\) \begin{equation} |A| = \sum_{i=1}^{n} a_{ij} C_{ij} \;\; \textrm{for any} \; 1 \leq j \leq n \end{equation}
Practical Example. For \(A=\begin{bmatrix}-1 & 5 & -2\\-6 & 6 & 0\\3 & -7 & 1\end{bmatrix},\) we will use row 1 to calculate \(|A|.\)
\begin{align} \begin{split} |A| &= a_{11} C_{11} + a_{12} C_{12} + a_{13} C_{13} \\ &= a_{11} M_{11} + a_{12}\,\textrm{-}M_{12} + a_{13} M_{13} \\ &= -1 \begin{vmatrix} 6 & 0 \\ -7 & 1 \end{vmatrix} -5\ \begin{vmatrix} -6 & 0 \\ 3 & 1 \end{vmatrix} -2 \begin{vmatrix} -6 & 6 \\ 3 & -7 \end{vmatrix}\\ &= -6 + 30 -48\\ &= -24 \end{split} \end{align}
The same result would result from using columns, for example, the second column.
\begin{align} \begin{split} |A| &= a_{12} C_{12} + a_{22} C_{22} + a_{23} C_{23} \\ &= a_{12}\,\textrm{-}M_{12} + a_{22} M_{22} + a_{23}\,\textrm{-}M_{23} \\ &= -5 \begin{vmatrix} -6 & 0 \\ 3 & 1 \end{vmatrix} + 6 \begin{vmatrix} -1 & -2 \\ 3 & 1 \end{vmatrix} + 7 \begin{vmatrix} -1 & -2 \\ -6 & 0 \end{vmatrix}\\ &= 30 + 30 - 84\\ &= -24 \end{split} \end{align}
What happens is \(n\) were larger, for example, \(n=4.\) Now, the minors \(M_{ij}\) are no longer \(2 \times 2\) determinants, so they cannot be calculated directly. Instead, they must undergo another round of cofactor calculation to obtain their determinant. This can then be inserted into a four-value cofactor sum to generate the overall determinant of \(A.\) As \(n\) grows, the number of iterations of cofactor calculation grows with it. As with inverses, once \(n > 2\) (or even for \(n = 2\)) we normally use a Python or R library to calculate the determinant. Consider \(A\) from the previous example.
As in the \(2 \times 2\) case, the determinant of \(A\) together with the cofactors of \(A\) are used to calculate the inverse \(A^{-1},\) if it exists. We begin by defining the cofactor matrix \(\mathbf{C}.\) \begin{equation} \mathbf{C} = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ C_{n1} & C_{n2} & \cdots & C_{nn} \end{bmatrix} \end{equation}
We then use \(\mathbf{C}\) to define the adjoint of \(A,\) \(\textrm{adj}(A) = A^{\ast} = \mathbf{C}^{T}.\) The following relationship between \(A,\) \(A^{\ast},\) and \(|A|\) exists. \begin{equation} \label{eq:adjoint} A \, A^{\ast} = |A| \, I \end{equation}
Eqn \eqref{eq:adjoint} can easily be rewritten to define \(A^{-1}.\) \begin{equation} A^{\ast} = A^{-1} \, |A| \, I \quad \Rightarrow \quad A^{-1} = \frac{1}{|A|} \, A^{\ast} \end{equation}
As before, as long as determinant \(|A| \neq 0,\) \(A\) is invertable.
Eigenvectors and their corresponding eigenvalues are special vectors and scalars related to a square matrix \(A.\) Eigen decomposition can be viewed as a form of factorization, although it is slightly different than the \(A = LU\) that we saw previously. Here, for an eigenvector \(\vec{u}\) and a corresponding scalar eigenvalue \(\lambda,\) \(\vec{u}\) and \(\lambda\) satisfy the eigen equation. \begin{equation} \label{eq:basic_eigen} A\,\vec{u} = \lambda\,\vec{u}\ \end{equation}
If \(A\) performs an operation on \(\vec{u}\) identical to a scalar \(\lambda,\) then \(A\) is changing the length of \(\vec{u},\) but it is not changing the direction of \(\vec{u}.\) We often rewrite Eqn \ref{eq:basic_eigen} to make it easier to solve. \begin{align} \label{eq:standard_eigen} \begin{split} A \vec{u} &= \lambda I \vec{u}\\ (A - \lambda I) \vec{u} &= 0 \end{split} \end{align}
Practical Example. Consider \(A = \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix}.\) To solve for \(\lambda\) in \eqref{eq:standard_eigen}, we first calculate the determinant \(|A - \lambda I| = \begin{vmatrix} (0.8 - \lambda) & 0.3 \\ 0.2 & ( 0.7 - \lambda) \end{vmatrix} = \lambda^{2} - \frac{3}{2}\lambda + \frac{1}{2} = (\lambda - 1) (\lambda - \frac{1}{2}).\) Equating \(|A - \lambda I| = 0\) gives us the two eigenvalues \(\lambda_1 = 1\) and \(\lambda_2 = \frac{1}{2}.\) We can now use \(\lambda_1\) and \(\lambda_2\) to solve for our two eigenvectors \(\vec{u}\) and \(\vec{v}.\) \begin{align} \begin{split} (A - \lambda_1 I) \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} &= \mathbf{0}\\ \left( \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right) \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} &= \mathbf{0}\\ \begin{bmatrix} -0.2 & 0.3 \\ 0.2 & -0.3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \mathbf{0} \end{split} \end{align}
Solving the quadratic equation \(a x^{2} + b x + c\) (\(a \neq 0\) otherwise this is not a valid quadratic equation) for two real-valued roots \(r_1\) and \(r_2\) uses a standard formula that leverages the following rules about the solutions.
If we input our \(a=1, b=-1.5, c=0.5\) from Eqn
\eqref{eq:standard_eigen} the eqn_roots() function
returns r1=1, r2=0.5, exactly as expected.
At this point you should recognize that the rows in the matrix are dependent, since row two is \(-1\) times row one. Solving one equation and two unknowns will give an infinite number of solutions. \begin{align} \begin{array}{r c r c c} \begin{matrix} -0.2 x_1 + 0.3 x_2 = 0 \\ \hfill 0.2 x_1 - 0.3 x_2 = 0 \end{matrix} & \quad \Longrightarrow \quad & \begin{matrix} -0.2 x_1 + 0.3 x_2 = 0 \\ \hfill 0 = 0 & \end{matrix} \quad \Longrightarrow \quad & x_1 = \frac{3}{2} x_2 \end{array} \end{align}
Any \(x_1, x_2\) that satisfy \(x_1 = \frac{3}{2} x_2\) can act as eigenvector \(\vec{u}.\) Notice this is true because any \([x_1, x_2]^{T}\) points in an identical direction. Only the length of the vector changes. For simplicity, we will choose \(\vec{u} = [1.5, 1]^{T},\) but any \(c \, [1.5, 1]^{T}\) would work. For \(\lambda_2\) we follow an identical strategy. \begin{align} \begin{array}{r c r c c} \begin{matrix} 0.3 x_1 + 0.3 x_2 = 0 \\ \hfill 0.2 x_1 + 0.2 x_2 = 0 \end{matrix} & \quad \Longrightarrow \quad & \begin{matrix} 0.3 x_1 + 0.3 x_2 = 0 \\ \hfill 0 = 0 & \end{matrix} \quad \Longrightarrow \quad & x_1 = -x_2 \end{array} \end{align}
Again, any \(x_1, x_2\) that satisfies \(x_1 = -x_2\) can act as an eigenvector to \(\vec{v}.\) We select a simple choice of \(\vec{v} = [1, -1]^{T}.\) In conclusion, two eigenvectors and two corresponding eigenvalues are defined for \(A:\) \(\vec{u} = \begin{bmatrix} 1.5\\1 \end{bmatrix}, \lambda_1 = 1,\) and \(\vec{v} = \begin{bmatrix} 1\\-1 \end{bmatrix}, \lambda_2 = \frac{1}{2}.\) We can confirm the eigenvector and eigenvalues are correct by confirming \(A \vec{u} = \lambda_1 \vec{u}.\) \begin{align} \begin{split} A\vec{u} &= \lambda_1 \vec{u}\\ \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \begin{bmatrix} 1.5\\1 \end{bmatrix} &= 1 \begin{bmatrix} 1.5\\1 \end{bmatrix}\\ \begin{bmatrix} (0.8)(1.5) + (0.3)(1)\\(0.2)(1.5) + (0.7)(1) \end{bmatrix} &= \begin{bmatrix} 1.5\\1 \end{bmatrix}\\ \begin{bmatrix} 1.5\\1 \end{bmatrix} &= \begin{bmatrix} 1.5\\1 \end{bmatrix} \end{split} \end{align} A similar check will show the same holds true for \(\vec{v}\) and \(\lambda_2.\)
As before, we rarely calculate eigenvectors and eigenvalues by hand.
In Python, the eig function return the eigenvalues and
eigenvectors for a square matrix \(A.\) In R, the eigen
function performs the same operation.
Take special notice, even though Python generally uses row-major
representations, the results of eig specify the
eigenvectors as \(n\)-valued lists, one for each eigenvector. The
first eigenvector returned by Python is therefore \(\vec{u_1} =
\begin{bmatrix} 0.83205029 & 0.5547002 \end{bmatrix}^{T}.\) This can
be easily confirmed by looking at the eigenvectors returned by R.
Singular value decomposition (SVD) factorizes or decomposes a matrix \(A\) into a set of orthogonal basis axes for both the row space and the column space of \(A.\) The row space of \(A\) is the span (the set of all possible linear combinations) of the rows of \(A.\) Similarly, the column space is the span of the columns of \(A.\)
To understand SVD, we need to discuss orthogonal matrices, symmetric matrices, and orthogonal diagonalization.
\(A\) is an orthogonal matrix if: (1) it is square or \(n \times n\); (2) its row vectors are orthonormal, and (3) its column vectors columns are orthonormal. Recall that a set of vectors is orthonormal if all pairs are orthogonal (they are perpendicular so their dot product is 0) and normalized (every vector is unit length). Given this, for orthogonal matrix \(A\) we have the following properties.
The first four properties follow directly from the fact that \(A\) rows and columns are orthonormal. The fifth property can be seen by recognizing that \(A^{T}\) swaps rows and columns, so \(A^{T} A\) takes the dot product of two rows \(A_{i \ast}\) and \(A_{j \ast}.\) This will be zero unless \(i = j,\) producing a matrix with zeros everyone except the diagonal. This is the definition of \(I.\) Finally, it follows that if \(A^{T} A = I\) then \(A^{T}\) must be \(A^{-1}.\)
\(A\) is symmetric if it is square and \(A=A^{T},\) that is, \(a_{ij} = a_{ji} \; \forall \; 1 \leq i,j \leq n.\)
\(A\) can be orthogonally diagonalized if there is an orthogonal matrix \(P\) s.t. \(P^{-1} A P = P^{T} A P = D\) where \(D\) is a diagonal matrix. The most common \(P\) and \(D\) come from the eigenvectors and eigenvalues of symmetric matrix \(A.\) \(P\) is a matrix whose columns are the eigenvectors of \(A.\) \(D\) is a diagonal matrix whose diagonal entries are the eigenvalues that correspond, in order, to the columns (eigenvectors) in \(P.\)
Practical Example. Consider eigenvectors and eigenvalues \(\vec{u} = \begin{bmatrix} 0.7630 \\ 0.6464 \end{bmatrix},\) \(\vec{v} = \begin{bmatrix} -0.6464 \\ 0.7630 \end{bmatrix},\) \(\lambda_1 = 1.0541,\) and \(\lambda_2 = 0.4459\) for matrix \(A = \begin{bmatrix} 0.8 & 0.3 \\ 0.3 & 0.7 \end{bmatrix}.\) \begin{align} \begin{split} P = \begin{bmatrix} 0.7630 & -0.6464 \\ 0.6464 & 0.7630 \end{bmatrix}; \;\;\; P^{-1} &= P^{T} = \begin{bmatrix} 0.7630 & 0.6464 \\ -0.6464 & 0.7630 \end{bmatrix}; \;\;\; D = \begin{bmatrix} 1.0541 & 0 \\ 0 & 0.4459 \end{bmatrix}\\[8pt] P^{-1} A P &= \begin{bmatrix} 0.7630 & 0.6464 \\ -0.6464 & 0.7630 \end{bmatrix} \begin{bmatrix} 0.8 & 0.3 \\ 0.3 & 0.7 \end{bmatrix} \begin{bmatrix} 0.7630 & -0.6464 \\ 0.6464 & 0.7630 \end{bmatrix}\\ &= \begin{bmatrix} 0.8043 & 0.6814 \\ -0.2882 & 0.3402 \end{bmatrix} \begin{bmatrix} 0.7630 & 0.6464 \\ -0.6464 & 0.7630 \end{bmatrix}\\ &= \begin{bmatrix} 1.0541 & 0 \\ 0 & 0.4459 \end{bmatrix} = D\\ \end{split} \end{align}
Let \(A\) be an \(n \times m\) matrix. SVD uses eigenvectors and eigenvalues of \(A^{T} A,\) since this is by definition symmetric. A symmetric matrix is guaranteed to be orthogonally diagonalizable. Given eigenvalues \(\lambda_1, \lambda_2, \ldots, \lambda_n\) for \(A^{T} A\) the singular values \(\sigma\) are defined as \(\sigma_1 = \sqrt{\lambda_1}, \sigma_2 = \sqrt{\lambda_2}, \ldots \sigma_n = \sqrt{\lambda_n}.\) Next, we substitute the singular values into the equation \(A \vec{v_i} = \sigma_i \vec{u_i}\) where \(\vec{v_i}\) is the \(i^{\textrm{th}}\) eigenvector of \(A^{T} A.\) Values of \(A, \vec{v_i},\) and \(\sigma_i\) are known. We use these to solve for \(\vec{u_i}.\)
Practical Example. Working again with \(A = \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix},\) we must find the eigenvectors and eigenvalues of \(A^{T} A\ = \begin{bmatrix} 0.68 & 0.38 \\ 0.38 & 0.58 \end{bmatrix}.\) Python is used to calculate \(\vec{v_1} = \begin{bmatrix} 0.7518 \\ 0.6594 \end{bmatrix}, \vec{v_2} = \begin{bmatrix} -0.6594 \\ 0.7518 \end{bmatrix}, \sigma_1=\sqrt{1.0133}=1.0067,\) and \(\sigma_2=\sqrt{0.2467}=0.4967.\) These values allow us to derive \(\vec{u_1}\) and \(\vec{u_2}.\) \begin{align} \begin{split} 1.0067\,\vec{u_1} &= A \vec{v_1}\\ &= \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \begin{bmatrix} 0.7518 \\ 0.6594 \end{bmatrix}\\ &= \begin{bmatrix} 0.7993 \\ 0.6119 \end{bmatrix}\\ \vec{u_1} &= \begin{bmatrix} 0.7939 \\ 0.6079 \end{bmatrix}\\[8pt] 0.4967\,\vec{u_2} &= A \vec{v_2}\\ &= \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \begin{bmatrix} -0.6594 \\ 0.7518 \end{bmatrix}\\ &= \begin{bmatrix} -0.3020 \\ 0.3944 \end{bmatrix}\\ \vec{u_2} &= \begin{bmatrix} -0.6080 \\ 0.7940 \end{bmatrix} \end{split} \end{align}
How can we interpret these initial SVD steps? Since \(\vec{v_1}\) and \(\vec{v_2}\) in our practical example are orthogonal, they form a basis that spans \(\mathbb{R}^{2}.\) In the general case, \((\vec{v_1}, \ldots, \vec{v_n})\) span \(\mathbb{R}^{n}.\) \(\vec{u_1}\) and \(\vec{u_2}\) are also normal and orthogonal, so they also form a basis that spans \(\mathbb{R}^{2}.\) This means that the steps we performed transform points between two different bases in \(\mathbb{R}^{2}.\) The points may spin about the origin, and they may move closer or farther apart from one another, but their relative distances and directions do not change. Intuitively, we are projecting points from one plane defined by \((v_1,v_2)\) to a second plane defined by \((u_1,u_2).\)
To complete the SVD, we define \(U=\begin{bmatrix} u_{1,x} & u_{2,x} \\ u_{1,y} & u_{2,y} \end{bmatrix},\) \(V^{T}=\begin{bmatrix} \vec{v_{1,x}} & \vec{v_{1,y}} \\ v_{2,x} & v_{2,y} \end{bmatrix},\) and \(D=\begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \end{bmatrix}.\) We use \(U, D,\) and \(V^{T}\) to combine our original \(A \vec{v_i} = \sigma_i \vec{u_i}\) equations. \begin{align} \begin{split} AV &= UD\\ (AV)V^{T} &= UDV^{T}\\ A(VV^{T}) &= UDV^{T}\\ AI &= UDV^{T}\\ A &= UDV^{T} \end{split} \end{align}
We have factored \(A\) into \(UDV^{T}.\) \(A\) is subdivided into a triple matrix multiplication consisting of a diagonal matrix \(D\) and two orthogonal matrices \(U\) and \(V^{T}.\)
Not surprisingly, both Python and R have built-in SVD functions.
Notice that Python returns \(-u_1\) versus our calculation of \(u_1\) (remember, the \(u_i\) are returned as the columns of \(U\) in Python), but this is still identical in that Python's \(u_1\) has the same length and is flipped about the \(xy\) axes, so there are equivalent eigenvectors. The same is true for Python's \(v_{11}\) and \(v_{12},\) the \(x\)-components of \(v_1\) and \(v_2.\) Here, negating the values flips the eigenvectors about the \(y\)-axis, but does not change the length, so the eigenvectors are again identical. R returns exactly the same \(U\) and \(V\) as Python, so clearly they are using an identical approach to eigen decompose \(A.\)
One interesting property of SVD is that each eigenvector represents a line that passes through values (samples) in \(A\) such that it minimizes error (or in SVD terminology, captures variance). If we order the eigenvectors by their largest to smallest eigenvalues, we obtain 1D, 2D, 3D, \(\ldots\) bases that maximize the amount of variance captured for the given \(n\) basis vectors. Eigenvalues are often very small, so we can keep only a few high-value eigenvalues and their corresponding eigenvectors and build a new matrix \(A^{\prime}\) from this reduced eigenset. Now \(A^{\prime}\) estimates \(A\) with factorized matrices \(U^{\prime}, D^{\prime}, V^{T\,\prime} \ll U, D, V^{T},\) but that still captures most of the variation in the original \(A\) (i.e., \(A^{\prime}\) is an accurate estimate of \(A\)).
The following Python program uses OpenCV (an open source computer vision library) to read a JPEG image and convert it to greyscale. A greyscale image is equivalent to a rectangular \(A\) where each entry is the greyscale brightness of a pixel in the image, usually on the range \(0 \ldots 255.\)
The original image is \(638 \times 960\) pixels. Normally, we view the rows of a matrix \(A\) of data as samples, and the columns as attribute values for each sample. In this context, we have 638 samples, or components, as they're sometimes called in computer vision. Each component is made up of 960 attribute values, or pixel brightness values on the range \(0, \ldots, 255\). SVD decomposes the image represented by \(A\) into \(U\), a \(638 \times 638\) matrix whose columns are orthonormal, \(D\), a diagonal matrix of the singular values of \(A\) in decreasing size, and \(V^{T}\), a second matrix of size \(960 \times 960\) whose columns are again orthonormal.
Given this, how are we "compressing" the image? Think of the process as follows.
Suppose we reduce \(A\) by maintaining the top 500, 400, 300, 200, or 100 eigenvectors, then display the compressed image. I think you will agree it is very difficult to see differences between the original image and the image reduced to 100 components. The best description might be that the reduced image looks "softer" than the original. This makes sense, since edges in an image are areas that violate the intuition that neighbouring pixels are similar, and therefore are the ones most likely to be less accurate when we compress the image.

How much space do we save by reducing the number of eigenvectors? The original \(A\) used \(U=n \times n=368^{2}=407,044\) values, \(D=n \times n=407,044\) values, and \(V^{T}=m \times m=960^{2}=921,600\) values, or \(A=1,735,688\) values. The \(n^{\prime}=100\) component image uses only \((638 \times 100) + (100 \times 100) + (100 \times 960)=169,000\) values, a \(90.3\%\) reduction.
You should download
the beach.jpg image used in the
code, then update the line that starts
img = cv.imgread to point to the location where you
saved your version of the beach image.
As a quick clarification on this code, the @-sign is
shorthand in Python for matrix multiplication.
Principal component analysis (PCA) is another way of reducing a matrix \(A\) into a smaller estimation via projection. PCA identifies "principal" orthogonal directions through a set of data. These are the directions (or basis vectors) that that capture the maximum amount of variance in the data in descending order. PCA axes also transform samples of potentially correlated variables into a set of linearly uncorrelated variables. Although the initial method of obtaining the principal components is different from SVD, the techniques are closely related. To explore PCA, we will use the context of a real-world dataset. Matrix \(A\) with size \(m \times n\) is made up of \(m\) rows representing \(m\) samples and \(n\) columns representing \(n\) variables measured for each sample. For example, a dataset of peoples' ages, weights, and heights would have \(m\) rows for for the \(m\) people sampled, and \(n=3\) columns for the variables age, weight, and height. Every row represents one sample, the age, weight, and height for one person.
Given a matrix \(A,\) we use it compute a sample covariance matrix \(\mathrm{S}.\) Covariance measures the relationship between two variables. A positive covariance indicates the variables tend to move in the same direction. A negative covariance suggests the variables tend to move in opposite directions.
We normally assume the columns of \(A\) are centered about the origin, which is equivalent to saying each column's mean \(\overline{A_{\ast j}} = 0.\) If this is not true, we can easily adjust \(A\) to produce it. \begin{align} \begin{split} \overline{A_{\ast j}} &= \frac{1}{m}\sum_{i=1}^{m} a_{ij}, 1 \leq j \leq n\\ A &= \begin{bmatrix} (a_{11} - \overline{A_{\ast 1}}) & (a_{12} - \overline{A_{\ast 2}}) & \cdots & (a_{1n} - \overline{A_{\ast n}})\\ (a_{21} - \overline{A_{\ast 1}}) & (a_{22} - \overline{A_{\ast 2}}) & \cdots & (a_{2n} - \overline{A_{\ast n}})\\ \vdots & \vdots & \ddots & \vdots \\ (a_{m1} - \overline{A_{\ast 1}}) & (a_{m2} - \overline{A_{\ast 2}}) & \cdots & (a_{mn} - \overline{A_{\ast n}})\\ \end{bmatrix} \end{split} \end{align}
The formula for the sample covariance between two variables \(X = [ x_1, x_2, \ldots, x_n ]\) and \(Y = [ y_1, y_2, \ldots, y_n ]\) computes the average product of deviation from each variable's mean \(\overline{x}\) and \(\overline{y}.\) \begin{equation} \label{eq:covar_XY} s_{ij} = \frac{\sum_{i=1}^{n} (x_i - \overline{x} ) ( y_i - \overline{y} )}{n} \end{equation}
Using Eqn \eqref{eq:covar_XY} we can compute the covariance between any row and column in \(A.\) We do this to generate the covariance matrix \(S.\) \begin{equation} S = \begin{bmatrix} s_{11} & s_{12} & \cdots & s_{1n} \\ s_{21} & s_{22} & \cdots & s_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ s_{m1} & s_{m2} & \cdots & s_{mn} \end{bmatrix} \end{equation}
One problem with the sample covariance matrix is that different variables use different units of measurement. This "weights" the variables against one another in ways that may not be ideal. A related concept to covariance is correlation \(\rho.\) Covariance measures total variation between two variables from their means. We can gauge the direction of the relationship, but not its strength, nor the dependency between the variables. Correlation measures the strength of the relationship between the variables. It uses a scaled measure of covariance to produce a "pure" value independent of any units associated with \(X\) and \(Y.\) To generate a sample correlation matrix, we first standardize the columns in \(A,\) producing a matrix \(Z\) such that the mean \(\overline{Z_{\ast j}} = 0\) and the standard deviation \(\sigma({Z_{\ast j}}) = 1.\) The \(z\)-score is used to do this. \begin{align} \begin{split} z &= \frac{X - \mu}{\sigma}\\ z_{ij} &= \frac{a_{ij} - \overline{A_{\ast j}}}{\sigma({A_{\ast j})}}, j \leq 1 \leq n \end{split} \end{align}
Given the \(n \times m\) matrix \(Z\,\) we use the entries \(z_{ij}\) to build an \(n \times n\) correlation matrix \(\mathrm{P}.\) \begin{equation} \mathrm{P} = \frac{Z^T Z}{n} \end{equation}
The correlation of a variable \(X\) with itself is 1, so the diagonals on the correlation matrix are also 1.
The link between PCA and linear algebra is in the singular values and singular vectors of \(A,\) which come from the eigenvalues \(\sigma_i = \sqrt{\lambda_i}\) and the eigenvectors \(u_i\) of the sample correlation matrix \(\textrm{P}.\) Given the total variance \(T = \sum_{i=1}^{n} \sigma_i^{2},\) and assuming the \(\sigma_i\) are sorted in descending order, then the first eigenvector \(u_1\) of \(\textrm{P}\) points in the most significant direction of the data, and captures (or explains) \(\frac{\sigma_1^{2}}{T}\) of the total variance. The second eigenvector \(u_2\) explains \(\frac{\sigma_2^{2}}{T}\) of the total variance, and so on. We normally stop when the fractions fall below a predefined threshold. If \(r\) eigenvectors are retained, we say the effective rank of \(A\) is \(r.\) Once we have selected \(r,\) we create a PCA matrix whose columns are the eigenvectors \(u_1 \ldots u_{r},\) then multiple it against \(S\) (the standardized version of \(A\)) to produce a reduced-size \(n \times r\) projection of \(A^{\prime}.\) \begin{equation} A^{\prime} = S \begin{bmatrix} u_1^{T} & \cdots & u_r^{T} \end{bmatrix} \end{equation}
As a practical example of PCA, we will apply it to the University of Wisconsin Breast Cancer dataset. This dataset contains 569 samples of image analysis results, as well as whether breast cancer was found or not. Ten image properties of the cell nuclei under examination are included: radius, texture, perimeter, area, smoothness, compactness, concavity, number of concave points, symmetry, and fractal dimension. Both the mean and standard error are provided for each of the ten image properties, producing a total of 20 predictor variables and one target variable (tumor presence or absence).
Since we are working with PCA, our goal here is to take the predictor variables and project them in a way that identifies important variables. This allows us to reduce the size of the dataset either by: (1) removing irrelevant variables; or (2) using PCA axes with large eigenvalues (maximizing variance capture) to replace the original variables. Using PCA will also identify and remove colinearity: variables that are highly correlated to one another.
As a starting point, we will load the dataset in CSV format in Python, and perform a series of preprocessing steps to produce a correlation matrix. You can download a copy of the dataset here.
Note that statsmodel allows us to request that PCA
standardize the input data during processing. This
produces variables with a mean \(\mu=0\) and a variance
\(\sigma^{2}=0.\) This is equivalent to centering and converting a
covariance matrix into a correlation matrix.
We can examine the correlation matrix for dark blue cells. A dark blue cell means the corresponding variables have a strong linear relationship (a strong correlation with one another).
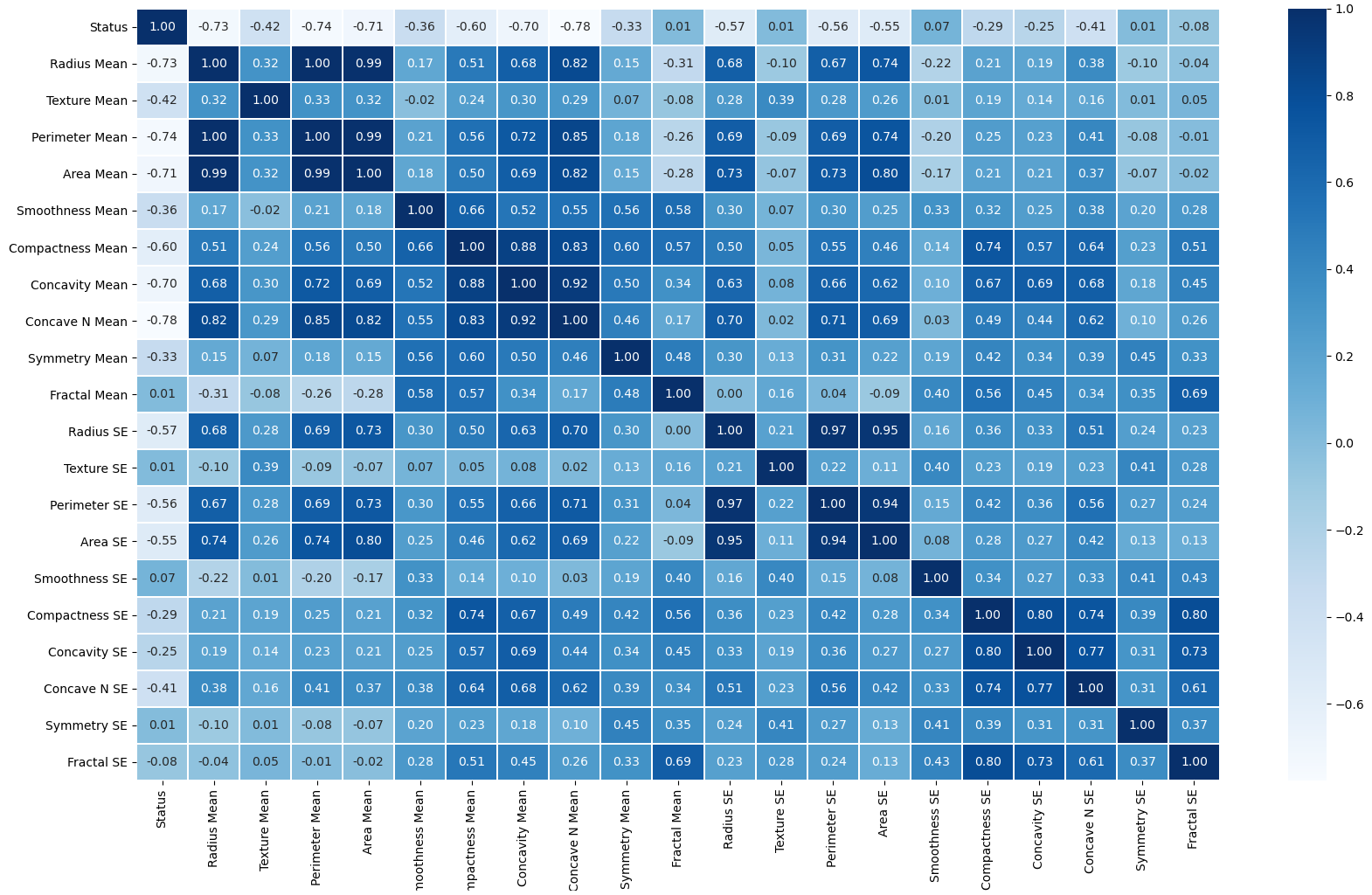
Cells along the diagonals are dark blue, but this makes sense
since a variable correlated with itself produces a perfect
correlation of \(1.0.\) More interesting are cells
like Perimeter Mean–Radius Mean
or Concave N Mean–Perimeter Mean. The first
correlation makes sense: the nulcli's perimeter mean is correlated
to its radius mean. The second is more interesting: the number of
concave "depressions" in the nucli is correlated with its
perimeter.
Another interesting exploration is the correlation between the variables and the PCA axes.
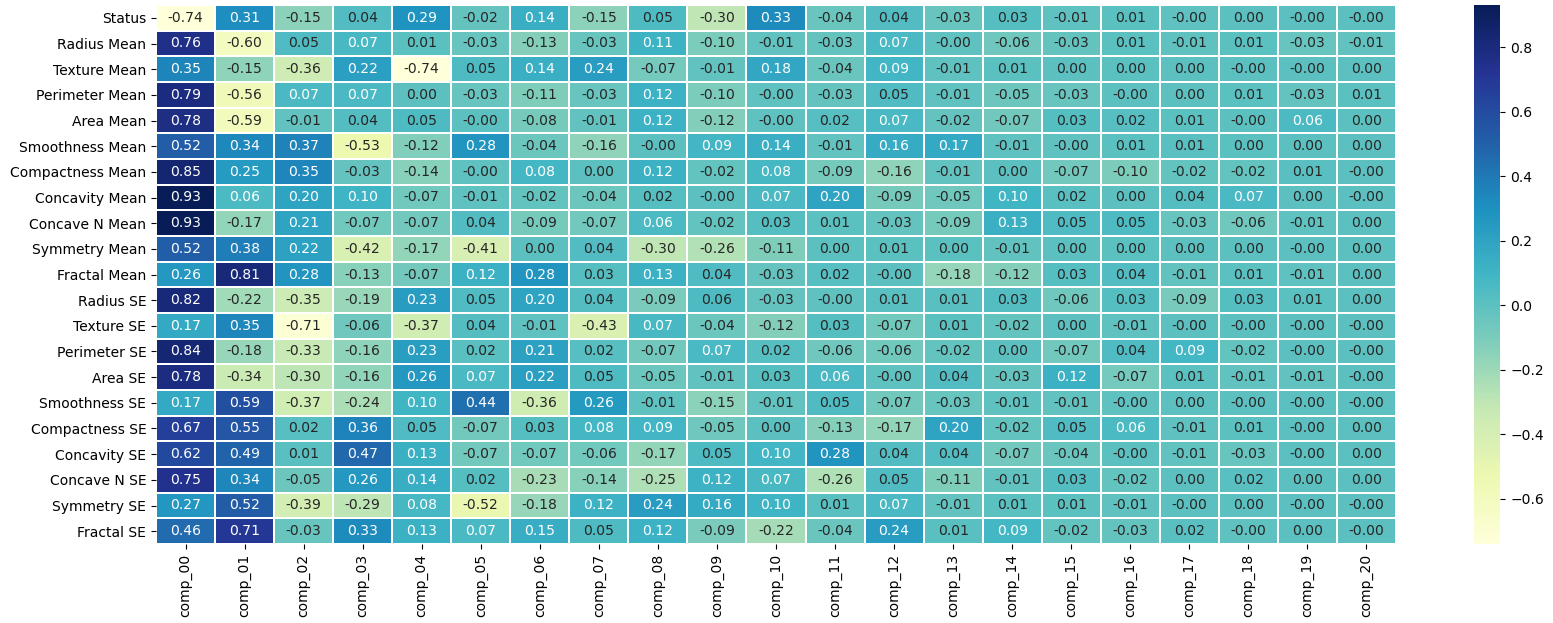
Here, we see visual confirmation of the fact that the PCA axes capture the maximum (remaining) variance in order from first to last. The first PCA axis is highly correlated with at least ten variables. The second PCA axis is highly correlated with only two variables. PCA axes after the second do not show the same level of correlation for any of the variables.
You should also recognize that PCA trades off data reduction for interpretability. We can replace twenty variables with only two or three PCA axes that are linear combinations of the variables' values. However, what those axes actually mean, in terms of the original variables, is often difficult or impossible to describe.
One way to try to understand how variables are being combined to generate PCA axes is to examine the loadings or weight coefficients used to combine variable values into an axis value.
The loadings for the first two principal components show
that Status captures more information in the first
principal component than the second. A number of the standard
error values like Texture SE,
Smoothness SE, Compactness SE,
and Symmetry SE do the same. What does this mean? It
tells us something about which variables are participating in
capturing the maximum amount of variance in the dataset.
Consultation with domain experts may provide more insight into
whether this combination of variables means something insightful.
A final use for the PCA results is dimensional reduction, that is, a re-representation of the dataset using (a few) PCA axes rather than then original twenty variables. Explained variance is the most common way to achieve this. A threshold variance cut-off (often 80% to 90%) is selected, and PCA axes are retained only until their cumulative variance capture meets or exceeds the threshold.
We achieve a cumulative variance of greater than 80% with only five principal component. Seven principal components returns a cumulative variance of greater than 90%.
Cumulative variance is not the only way to choose the number of PCA axes to retain. Another is the Kaiser criterion, where we include principal components only if their eigenvalues are greater than 1. Remember that each eigenvalue is associated with an eigenvector, which is one of the principal components.
Using the Kaiser criterion, we would actually keep nineteen of the twenty PCA axes, which provides only a minimum reduction in data.
A final, more visual approach is to generate a scree plot of the eigenvalues, and search for an "elbow" in the plot. We only include PCA axes that occur up to the elbow.
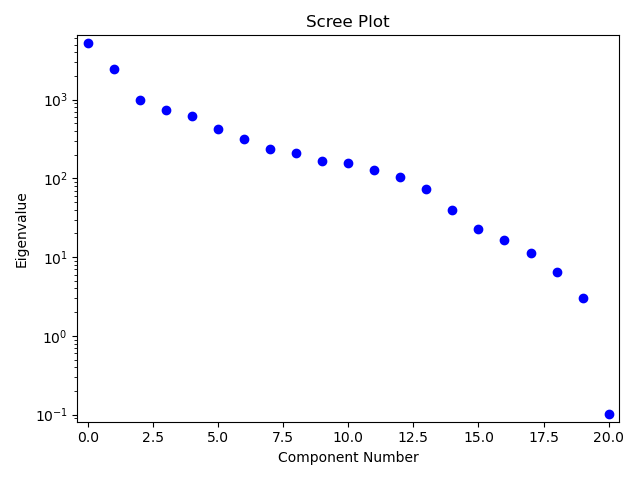
The scree plot suggests only the first three PCA axes need to be retained.
I initially mentioned that PCA and SVD are closely related. Intuitively, you can see that both are methods to project data onto a set of orthogonal basis vectors. The difference is that PCA is normally described through the use of covariance and correlation matrices, where SVD is described using eigenvectors and eigenvalues. For a matrix \(A,\) SVD factorizes \(A\) into \(A = UDV^{T}.\) Although we will not go through the proof here, it can be shown that, for a given matrix \(A,\) its standardized form \(S\) is equivalent to its factorization. \begin{equation} S = UDV^{T} \end{equation}
One immediate consequence of this is that you can compute the SVD of
\(A\) to get its principal components, rather than using covariance.
In fact, most PCA libraries use SVD rather than covariance, since it
is normally faster. This is also why Python's
statsmodel library offers an argument in
its PCA function to allow you to choose eig
or svd to solve for the principal components.
One use of PCA is to support efficient and accurate clustering. Clustering a dataset with a large number of variables is problematic. For a high-dimensional dataset two samples \(x_1\) and \(x_2\) have large differences in most dimensions. This means only a small number of dimensions will be used to define similarity, and those values are often overwhelmed by the large number of highly dissimilar dimensions. To overcome this, we project into a much lower-dimensional space (e.g., \(\mathbb{R}^{2}\) or \(\mathbb{R}^{3}\)) prior to building similarities between samples. PCA offers an effective way to perform the projection, since it maximizes the capture of variance per additional axis, and therefore should ensure the estimate similarity between \(x_1\) and \(x_2\) is close to the actual similarity in the original \(\mathbb{R}^{n}\) space.
As an initial example of this approach, we will use the famous Iris dataset collected by Ronald Fisher. Fisher measured the petal widths and lengths, and the sepal widths and lengths of fifty examples of three types of irises: Iris setosa, Iris virginica, and Iris versicolor. To test PCA cluster, we will perform the following steps.
In reality, we would never do this, since we know that petal length and petal width already do an excellent job of separating the irises in 2D spatial clusters. Consider the scatterplot below, showing the three types of irises identified by color, with the \(x\)-axis representing petal length and the \(y\)-axis representing petal width.
Our hope for converting from the original variables to PCA axes is that we can obtain a significant data reduction with an acceptable loss in accuracy. Since we are potentially "throwing information away" when we project with PCA, intuitively we would not expect to maintain the original level of accuracy.
The following R and Python code loads the iris dataset and divides it into stratified training and test sets (the same relative percentage of classes exist in both training and test). k nearest neighbours (KNN) clustering is applied to the training data. We then compute the first two PCA axes on the training data, and use them to project the test data into a PCA-projected test set. KNN is then applied to the PCA-projected test set. Finally, since we know the correct iris type for each test sample, we can compute the accuracy of both the original and PCA-projected test results. Results showed one misclassification (of 50 samples) using the four original axes, and one misclassification for the two PCA axes. We can discard 50% of the data while still maintaining an identical accuracy rate.
As an example of a more "difficult" dataset, we will use the load
dataset from a previous year's summer practicum representing loan
grades A through F and good–bad categories depending on loan
grade. From the original
variables we remove any non-categorical variable and variables
with more than 50% missing values, convert any remaining missing
values to 0, then use loan grade as the target, leaving 42
predictors. We also modify the predictor loan grade in two ways:
first, in its original A–F format (samples with loan grades
of G were removed from the data) and in a binary
format where grades A, B, and
C were "good" and grades D, E,
and F were "bad." Using all 42 axes in their
original format together with k nearest neighbours (KNN)
clustering produced accuracies of 66.3% and 92.2%, respectively. We
then ran incremental PCA (required due to memory constraints). The
table below shows variance captured and accuracy for \(1, 2,
\ldots 15\) PCA axes.
| A,B,C,D,E,F | Good,Bad | |||
|---|---|---|---|---|
| Axes | Variance | Accuracy | Variance | Accuracy |
| 1 | 4.5% | 24.8% | 4.5% | 70.2% |
| 2 | 7.0% | 25.0% | 7.0% | 70.1% |
| 3 | 13.9% | 25.1% | 13.9% | 70.5% |
| 4 | 22.5% | 27.2% | 22.5% | 72.3% |
| 5 | 31.4% | 28.4% | 31.4% | 72.9% |
| 6 | 35.4% | 31.9% | 35.4% | 73.7% |
| 7 | 43.2% | 30.6% | 43.2% | 73.4% |
| 8 | 47.1% | 29.7% | 47.1% | 73.4% |
| 9 | 49.9% | 30.2% | 49.9% | 74.5% |
| 10 | 54.1% | 65.5% | 54.1% | 94.3% |
| 11 | 57.4% | 62.6% | 57.4% | 94.0% |
| 12 | 60.1% | 60.6% | 60.1% | 93.5% |
| 13 | 63.0% | 59.4% | 63.0% | 93.3% |
| 14 | 65.4% | 57.9% | 65.4% | 92.8% |
| 15 | 68.3% | 56.8% | 68.3% | 92.5% |
For the binary good–bad categorization, good performance is obtained even with one PCA axis. At approximately 50% variance captured, the accuracy jumps significantly from around 75% to around 95%, then stays steady as more axes are added. At least for this dataset, ten PCA axes produces excellent accuracy. This represents a reduction of \(887,380\) samples with \(72\) variables per sample \((63,891,360\) data points), to \(42\) variables per sample after preprocessing \((37,269,960\) data points), a 41.67% reduction, to \(10\) variables per sample \((8,887,380\) data points), an 86.1% reduction. Reducing data size by over 85% produces an increase in accuracy of approximately 2%.
When we move to the more complicated problem of predicting the actual loan grade from A through F, the original 42 axes produce an accuracy of 66.3%, which is actually very good. The table shows accuracies for PCA axes ranging from 1 to 15. As before, at ten PCA axes we begin to approach accuracy percentages rivaling the full 42-axis model.
We have spent extensive time discussing how to solve \(A\vec{x} = \vec{b}.\) Deriving \(A^{-1}\) and using Gaussian elimination or elimination matrices are some of the approaches we have presented. However, what happens when there is no solution to \(A\vec{x} = \vec{b}.\) This is not uncommon, for example, when \(A^{-1}\) is singular or the rows of \(A\) are not independent. In this case, we might choose to instead find the solution \(\vec{\hat{x}}\) that is the closest solution to \(A\vec{x} = \vec{b}.\) Since \(\vec{\hat{x}}\) is not the exact solution to the equation, it will produce an error or residual \(\vec{r} = A\vec{\hat{x}} - \vec{b}.\) Minimizing the residual \(\vec{r}\) will generate the best possible solution, since it minimizes the error in the \(\vec{\hat{x}}\) we select. \begin{align} \begin{split} \underset{\vec{\hat{x}} \in R^{m}}{\textrm{minimize}} ||A\vec{\hat{x}} - \vec{b}|| &= \textrm{min}\, ||A\vec{\hat{x}} - \vec{b}||^{2}\\ &= \textrm{min}\, ||\vec{r}||^{2}\\ &= \textrm{min}\, (r_1^{2} + r_2^{2} + \cdots + r_m^{2}) \end{split} \end{align}
This is known as the linear least squares problem, where \(A\) and \(\vec{b}\) are given as data, \(\vec{x}\) is the quantity to minimize, and \(||A\vec{x} - \vec{b}||\) is the objective function. Vector \(\vec{\hat{x}}\) satisfies the objective function if \(||A\vec{\hat{x}} - \vec{b}|| \leq ||A\vec{x} - \vec{b}||\) for all possible \(\vec{x}.\) Another name for this problem, which you are very familiar with, is regression. \(\vec{\hat{x}}\) is the result of regressing \(\vec{b}\) onto the columns of \(A.\) \begin{equation} ||A\vec{x} - \vec{b}||^{2} = ||(x_1 A_{1 \ast} + \cdots + x_n A_{\ast n} ) - b||^{2} \end{equation}
Practical Example. Given \(A = \begin{bmatrix} 2 & 0 \\ -1 & 1 \\ 0 & 2 \end{bmatrix}\) and \(\vec{b} = \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix},\) an over-determined set of three equations and two unknowns is formed. \begin{equation} 2 x_1 = 1 \qquad -x_1 + x_2 = 0 \qquad 2 x_2 = -1 \end{equation}
Simple examination shows \(x_1 = \frac{1}{2}\) from the first equation and \(x_2 = -\frac{1}{2}\) from the third equation does not satisfy the second equation \(-\frac{1}{2} + (-\frac{1}{2}) \neq 0.\) The least squares problem asks us to minimize \((2 x_1 - 1)^{2} + (-x_1 + x_2)^{2} + (2 x_2 + 1)^{2}.\) Since we have not discussed how to find the optimal solution, we provide it directly, \(\vec{\hat{x}} = [ \frac{1}{3}, -\frac{1}{3} ].\) This produces a residual \(\vec{r} = A \vec{\hat{x}} - \vec{b} = \begin{bmatrix} -\frac{1}{3} & -\frac{2}{3} & \frac{1}{3} \end{bmatrix},\) \(||r||^{2} = \frac{2}{3}.\)
Various methods exist for solving for \(\vec{\hat{x}}.\) We will start with a solution using partial derivatives. Given a function \(f(x) = ||A\vec{x} - \vec{b}||^{2},\) minimizing \(f\) requires the partial derivatives to be zero. \begin{equation} \frac{\partial f}{\partial x_i}(\vec{\hat{x}}) = 0 \; \forall \; 1 \leq i \leq n \end{equation}
This can be expressed in terms of the gradient \(\nabla f(x) = 0.\) The gradient can be expressed as a matrix. \begin{align} \begin{split} \nabla f(x) &= 2 A^{T}(A\vec{x} - \vec{b}) = 0\\ A^{T} A \vec{\hat{x}} &= A^{T} b\\ \vec{\hat{x}} &= (A^{T} A)^{-1} A^{T} b \end{split} \end{align}
If we assume the columns of \(A\) are linearly independent, then \(A^{T} A\) is invertable, so a unique solution exists for the least squares problem.
Alternatively, we can use a QR factorization to compute \(\hat{x}.\) Given \(A=QR\) for \(A\) with linearly independent columns, we can express the pseudo-inverse \(A^{\dagger}\) of \(A\) in terms of \(Q\) and \(R.\) \begin{align} \begin{split} A^{T} A &= (QR)^{T} (QR) = R^{T} Q^{T} Q R = R^{T} R\\ A^{\dagger} & = (A^{T} A)^{-1} A^{T} = (R^{T} R)^{-1} (QR)^T = R^{-1} R^{-T} R^{T} Q^{T} = R^{-1} Q^{T} \end{split} \end{align}
This allows us to define \(\hat{x} = A^{\dagger}b = R^{-1} Q^{T} b.\) To compute \(\hat{x},\) we multiply \(b\) by \(Q^{T},\) then compute \(R^{-1} (Q^{T} b)\) using back-substitution.
For matrix \(A = \begin{bmatrix} 3 & -2 \\ 0 & 3 \\ 4 & 4 \end{bmatrix}\) and \(b= \begin{bmatrix} 3 & 5 & 4 \end{bmatrix}^{T},\) solve for the solution \(\hat{\vec{x}}\) with the minimum residual \(r.\)
Solution \(\hat{\vec{x}} = \begin{bmatrix} 1.08 & 1.8 & 5.44 \end{bmatrix}^{T}\) is the "best" solution to the equation \(\begin{bmatrix} 3 & -2 \\ 0 & 3 \\ 4 & 4 \end{bmatrix} x = \begin{bmatrix} 3 \\ 5 \\ 4 \end{bmatrix}\) in that it minimizes the residual error \(r = 16.\)